

分析 (1)通过折起后AE⊥CD、EF⊥CD,及面面垂直的判定定理即得结论;
(2)过B作EF的延长线的垂线交EF于O点,连结OA,则∠BAO就是直线AB与平面AEF所成的角.通过余弦定理及勾股定理可得AB=$\frac{\sqrt{10}}{2}$a,在Rt△ABO中利用sin∠BAO=$\frac{BO}{AB}$计算即可.
解答 (1)证明:∵在Rt△ABC中,D为AB的中点,∠CAD=60°,∴AD=CD=DB,
又E是CD的中点,得AE⊥CD,折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE?平面AEF,EF?平面AEF,∴CD⊥平面AEF,
又CD?平面CDB,∴平面AEF⊥平面CBD;
(2) 解:由(1)知CD⊥平面AEF,
解:由(1)知CD⊥平面AEF,
过B作EF的延长线的垂线交EF于O点,连结OA,
∴OB∥CD,∴OB⊥平面AEF,
∴∠BAO就是直线AB与平面AEF所成的角.
设AC=a,在△CDB中,∠DCB=30°,CE=$\frac{a}{2}$,CB=$\sqrt{3}$a,
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=$\frac{7{a}^{2}}{4}$,
又AE=$\frac{\sqrt{3}}{2}$a,∴AB=$\sqrt{\frac{7{a}^{2}}{4}+\frac{3{a}^{2}}{4}}$=$\frac{\sqrt{10}}{2}$a,
又CF=$\frac{\frac{a}{2}}{cos30°}$=$\frac{\sqrt{3}}{3}$a,∴BF=$\sqrt{3}$a-$\frac{\sqrt{3}}{3}$a=$\frac{2\sqrt{3}}{3}$a,
∴BO=$\frac{2\sqrt{3}}{3}$asin60°=a,
∴sin∠BAO=$\frac{BO}{AB}$=$\frac{\sqrt{10}}{5}$,
∴直线AB与平面AEF所成角的正弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查空间中面面垂直的判定,以及求二面角的三角函数值,注意解题方法的积累,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:解答题
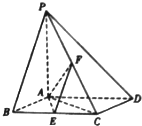 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的四个顶点所构成的菱形的边长是$\sqrt{5}$,面积是4,圆R:(x-4)2+y2=r2(6>r>2)与椭圆C交于点M与点N,连接RM并延长交椭圆于点P.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的四个顶点所构成的菱形的边长是$\sqrt{5}$,面积是4,圆R:(x-4)2+y2=r2(6>r>2)与椭圆C交于点M与点N,连接RM并延长交椭圆于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (-$∞,-\frac{\sqrt{3}}{2}$) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com