Question

7．平行六面体ABCD-A₁B₁C₁D₁中，∠A₁AD=∠A₁AB=60°，DAB=90°，A₁A=3，AB=2，AD=1，则其对角线AC₁的长为$\sqrt{23}$．

Answer 1

分析 直接利用后利用平面向量的数量积进行运算．

解答 解：如图，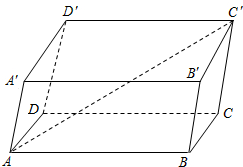

可得$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$=$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA′}$，
故$|\overrightarrow{AC′}{|}^{2}=（\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA′}）^{2}$=$|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AD}{|}^{2}+|\overrightarrow{AA′}{|}^{2}$$+2（\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AB}•\overrightarrow{AA′}+\overrightarrow{AD}•\overrightarrow{AA′}）$
=2²+1²+3²+2（2×1×0+2×3×$\frac{1}{2}$+1×3×$\frac{1}{2}$）=23．
∴AC′=$\sqrt{23}$．
故答案为：$\sqrt{23}$．

点评 本题考查了利用平面向量求解立体几何问题，考查了平面向量的数量积运算，是基础的计算题．