
已知函数f(x)=(ax+1)ex.
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[-2,0]上的最小值.
(1)见解析
(2)当a>1时,f(x)在区间[-2,0]上的最小值为-a·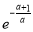 ;
;
当0<a≤1时,f(x)在区间[-2,0]上的最小值为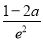 .
.
【解析】【解析】
依题意,函数的定义域为R,
f′(x)=(ax+1)′ex+(ax+1)(ex)′=ex(ax+a+1).
(1)①当a=0时,f′(x)=ex>0,
则f(x)的单调递增区间为(-∞,+∞);
②当a>0时,由f′(x)>0,解得x>-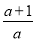 ,
,
由f′(x)<0,解得x<-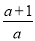 ,
,
则f(x)的单调递增区间为(-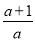 ,+∞),
,+∞),
f(x)的单调递减区间为(-∞,-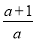 );
);
③当a<0时,由f′(x)>0,解得x<-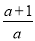 ,
,
由f′(x)<0解得,x>-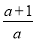 ,
,
则f(x)的单调递增区间为(-∞,-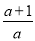 ),
),
f(x)的单调递减区间为(-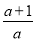 ,+∞).
,+∞).
(2)①当 时,
时,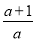 )上是减函数,
)上是减函数,
在(-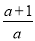 ,0)上是增函数,
,0)上是增函数,
则函数f(x)在区间[-2,0]上的最小值为f(-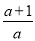 )=-a·
)=-a·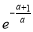 ;
;
②当 时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=
时,即当0<a≤1时,f(x)在[-2,0]上是增函数,则函数f(x)在区间[-2,0]上的最小值为f(-2)=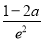 .
.
综上,当a>1时,f(x)在区间[-2,0]上的最小值为-a·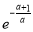 ;
;
当0<a≤1时,f(x)在区间[-2,0]上的最小值为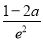 .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:选择题
已知一元二次不等式f(x)<0的解集为{x|x<-1或x>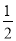 },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )
A.{x|x<-1或x>-lg2} B.{x|-1<x<-lg2}
C.{x|x>-lg2} D.{x|x<-lg2}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-2函数的单调性与最值(解析版) 题型:解答题
已知函数f(x)=x+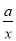 (x≠0,a∈R).
(x≠0,a∈R).
(1)当a=4时,证明:函数f(x)在区间[2,+∞)上单调递增;
(2)若函数f(x)在[2,+∞)上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:填空题
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,则f(-3)=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:选择题
已知函数f(x)的定义域为[3,6],则函数y= 的定义域为( )
的定义域为( )
A.[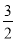 ,+∞) B.[
,+∞) B.[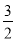 ,2)
,2)
C.(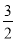 ,+∞) D.[
,+∞) D.[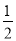 ,2)
,2)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:选择题
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=lnx-ax,若函数在定义域上有且仅有4个零点,则实数a的取值范围是( )
A.(e,+∞) B.(0,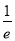 )
)
C.(1,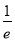 ) D.(-∞,
) D.(-∞,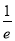 )
)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:选择题
经过原点且与曲线y=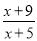 相切的方程是( )
相切的方程是( )
A.x+y=0或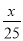 +y=0 B.x-y=0或
+y=0 B.x-y=0或 +y=0
+y=0
C.x+y=0或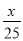 -y=0 D.x-y=0或
-y=0 D.x-y=0或 -y=0
-y=0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
随机变量X的概率分布规律为P(X=n)=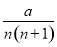 (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P(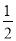 <X<
<X<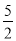 )的值为( )
)的值为( )
A.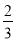 B.
B.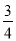 C.
C. D.
D.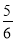
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com