
分析 (Ⅰ)由已知数列递推式可得当n≥2时,Sn=λSn-1+1.与原递推式作差可得an+1=λan,即n≥2时$\frac{{{a_{n+1}}}}{a_n}=λ$.验证a2=λa1,可得数列{an}是等比数列.结合已知求得λ值,则数列{an}的通项公式可求;
(Ⅱ)把(Ⅰ)中求得的通项公式代入bn=nan,整理后利用错位相减法求数列{bn}的前n项和.
解答 解:(Ⅰ)由Sn+1=λSn+1可知 当n≥2时,Sn=λSn-1+1.
作差可得an+1=λan,即n≥2时$\frac{{{a_{n+1}}}}{a_n}=λ$.
又a1=1,故a2=λa1.
∴数列{an}是等比数列.
由于a3=a1λ2=4,λ>0,解得λ=2.
数{an}的通项公式为:${a_n}={2^{n-1}}$;
(Ⅱ)由${a_n}={2^{n-1}}$,可知${b_n}=n•{2^{n-1}}$.
设数列{bn}前n项和为Tn,
则${T_n}=1•{2^0}+2•{2^1}+3•{2^2}+…+(n-1)•{2^{n-2}}+n•{2^{n-1}}$,①
$2{T_n}=1•2+2•{2^2}+…+(n-2)•{2^{n-2}}+(n-1)•{2^{n-1}}+n•{2^n}$,②
①-②得:$-{T_n}=1+2+{2^2}+…+{2^{n-2}}+{2^{n-1}}-n•{2^n}$=$\frac{1×(1-{2}^{n})}{1-2}-n•{2}^{n}$=2n-1-n•2n.
∴${T_n}=n•{2^n}-{2^n}+1$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:解答题
| 交易量X(件) | 150 | 180 | 200 | 250 | 320 |
频率 | $\frac{1}{12}$ | $\frac{1}{6}$ | a | $\frac{1}{4}$ | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
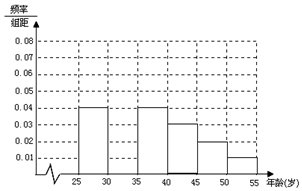 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com