
| A. | (-∞,-$\frac{1}{e}$) | B. | (-∞,-e) | C. | (e,+∞) | D. | ($\frac{1}{e}$,+∞) |
分析 先判断函数为偶函数,则要求函数f(x)有5个零点,只要求出当x>0时,f(x)有2个零点即可,分别y=ex与y=-ax的图象,利用导数的几何意义即可求出.
解答 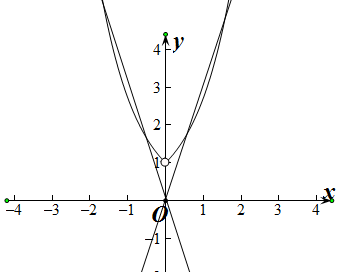 解:∵f(-x)=f(x),
解:∵f(-x)=f(x),
∴函数f(x)为偶函数,
∵当x=0,f(x)=0时,
∴要求函数f(x)有5个零点,
只要求出当x>0时,f(x)有2个零点即可,
分别y=ex与y=-ax的图象,如图所示,
设直线y=-ax与y=ex相切,
切点为(x0,y0),
∴y′=ex,
∴k=${e}^{{x}_{0}}$=$\frac{{e}^{{x}_{0}}}{{x}_{0}}$,
∴x0=1
∴-a=e,
∵当x>0时,f(x)有2个零点即可.
∴-a>e,
∴a<-e,
故选:B
点评 本题考查了函数零点的问题,以及函数的奇偶性,以及导数的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
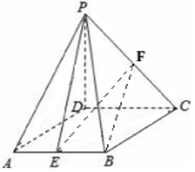 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
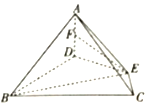 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com