
分析 (Ⅰ)根据动圆Q过定点A(2,0)且与y轴截得的弦MN的长为4,建立方程,即可求动圆圆心Q的轨迹C的方程;
(Ⅱ)设直线的方程为x=ny+m,代入y2=4x,利用韦达定理,结合kPA+kPB=2kPG,即可得出结论.
解答 解:(Ⅰ)设Q(x,y),根据题意得$\sqrt{|x{|}^{2}+{2}^{2}}=\sqrt{(x-2)^{2}+{y}^{2}}$,…(2分)
整理得y2=4x,所以动圆圆心Q的轨迹C的方程是y2=4x.…(4分)
(Ⅱ)设存在符合题意的定点G.
设直线的方程为x=ny+m(n≠0且n∈R),则G(m,0).…(5分)
将x=m+ny代入y2=4x,整理得y2-4ny-4m=0.
由题意得△=16n2+16m>0,即n2+m>0.
设A(x1,y1),B(x2,y2),则y1+y2=4n,y1y2=-4m,
${k_{PA}}=\frac{{{y_1}-1}}{{{x_{_1}}+2}}=\frac{{{y_1}-1}}{{\frac{{{y_1}^2}}{4}+2}}=\frac{{4({y_1}-1)}}{{{y_1}^2+8}}$,${k_{PB}}=\frac{{4({y_2}-1)}}{{{y_2}^2+8}}$,${k_{PG}}=\frac{1}{-2-m}=-\frac{1}{m+2}$,
由题意得kPA+kPB=2kPG,即kPA+kPB-2kPG=0,
所以$\frac{{2({y_1}-1)}}{{{y_1}^2+8}}+\frac{{2({y_2}-1)}}{{{y_2}^2+8}}+\frac{1}{m+2}=0$,…(7分)
即$2(m+2){y_1}{y_2}({y_1}+{y_2})+16(m+2)({y_1}+{y_2})+2[{({y_1}+{y_2})^2}-2{y_1}{y_2}](2-m)+{({y_1}{y_2})^2}-32m=0$…(9分)
把y1+y2=4n,y1y2=-4m代入上式,
整理得(m-2)n=(m+2)(2-m),…(11分)
又因为n∈R,所以$\left\{\begin{array}{l}(m+2)(2-m)=0\\ m-2=0\end{array}\right.$,解得m=2.
所以存在符合题意的定点G,且点G的坐标为(2,0).…(13分)
点评 本题考查抛物线方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | l1∥l2 | B. | l1⊥l2 | C. | l1和l2重合 | D. | l1,l2斜交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
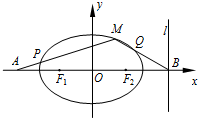 在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com