
分析 (1)通过在Sn=npan中令n=1可知p=1或a1=0并能排除p=1,进而重新令n=2计算即得结论;
(2)利用an=Sn-Sn-1整理可知$\frac{a_n}{{{a_{n-1}}}}=\frac{n-1}{n-2}({n≥3})$,通过累乘可知${a_n}=({n-1}){a_2}({n∈{N^*}})$,进而计算即得结论.
解答 解:(1)令n=1,则a1=pa1,
∴p=1或a1=0;
假设p=1,再令n=2,则a1+a2=2a2,
于是有a1=a2,这与题目a1≠a2矛盾,
∴必有a1=0,p≠1,a2≠0,
下面重新令n=2,则a1+a2=2pa2,
∵a1=0,a2≠0,
∴$p=\frac{1}{2}$;
(2)∵$p=\frac{1}{2}$,
∴${S_n}=\frac{n}{2}{a_n}$,${S_{n-1}}=\frac{n-1}{2}{a_{n-1}}$,
以上两式相减得:${a_n}=\frac{n}{2}{a_n}-\frac{n-1}{2}{a_{n-1}}({n≥2})$,
即:$\frac{a_n}{{{a_{n-1}}}}=\frac{n-1}{n-2}({n≥3})$,
采用累乘法可得:${a_n}=({n-1}){a_2}({n∈{N^*}})$,
又∵S10=45,
∴a10=9,
∴a2=1,
∴${a_n}=n-1({n∈{N^*}})$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
| 82 | 202 | 352 | 321 | 25 | 293 | 293 | 86 | 28 | 206 |
| 323 | 355 | 357 | 33 | 325 | 113 | 233 | 294 | 50 | 296 |
| 115 | 236 | 357 | 326 | 52 | 301 | 140 | 328 | 238 | 358 |
| 58 | 255 | 143 | 360 | 340 | 302 | 370 | 343 | 260 | 303 |
| 59 | 146 | 60 | 263 | 170 | 305 | 380 | 346 | 61 | 305 |
| 175 | 348 | 264 | 383 | 62 | 306 | 195 | 350 | 265 | 385 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
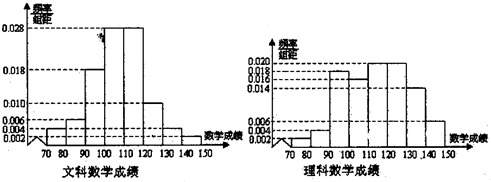
| 文科 | 理科 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 | 50 | 50 | 100 |
| P(K2>k) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+4$\sqrt{3}$ | B. | 5±4$\sqrt{3}$ | C. | 5-4$\sqrt{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com