Question

15．在锐角△ABC中，B=60°，|${\overrightarrow{AB}$-$\overrightarrow{AC}}$|=2，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围为（　　）

• A． （0，12）
• B． [${-\frac{1}{4}$，12）
• C． （0，4]
• D． （0，2]

Answer 1

分析 以B为原点，BA所在直线为x轴建立坐标系，得到C的坐标，找出三角形为锐角三角形的A的位置，得到所求范围．

解答 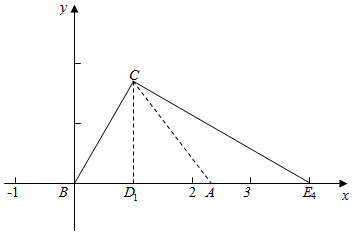解：以B为原点，BA所在直线为x轴建立坐标系，
∵B=60°，|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=2，
∴C（1，$\sqrt{3}$），
设A（x，0）
∵△ABC是锐角三角形，
∴A+C=120°，∴30°＜A＜90°，
即A在如图的线段DE上（不与D，E重合），
∴1＜x＜4，
则$\overrightarrow{AB}•\overrightarrow{AC}$=x²-x=（x-$\frac{1}{2}$）²-$\frac{1}{4}$，
∴$\overrightarrow{AB}•\overrightarrow{AC}$的范围为（0，12）．
故选：A．

点评 本题考查数量积的应用，根据向量数量积的模长公式，利用解析法建立坐标系，利用坐标法求数量积范围是解决本题的关键．综合性较强，有一定的难度．