Question

9．平面上有两条相距2a的平行线，把一枚半径为r（r＜a）的硬币任意掷在两线之间，则硬币不与任何一条直线相碰的概率是$\frac{a-r}{a}$．

Answer 1

分析 为了确定硬币的位置，由硬币中心O向靠得最近的平行线引垂线OM，垂足为M，这样线段OM长度|OM|的取值范围就是[0，a]，只有当r＜|OM|≤a时，硬币不与平行线相碰，最后根据几何概型的概率公式解之即可．

解答 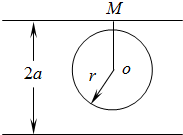解：把“硬币不与任一条平行线相碰”的事件记为事件A，
为了确定硬币的位置，由硬币中心O向靠得最近的平行线引垂线OM，垂足为M，
如图所示，这样线段OM长度|OM|的取值范围就是[0，a]，
只有当r＜|OM|≤a时，硬币不与平行线相碰，
所以所求事件A的概率就是$\frac{a-r}{a}$．
故答案为：$\frac{a-r}{a}$．

点评 本题主要考查了几何概型，解题的关键确定硬币的位置，同时考查了分析问题的能力，属于中档题