
分析 由题意得数列{an}的前15项为负数,第16项为0,从第17项开始为正值,
当n≤16时,数列{|an|}的前n项和Sn=-Tn;当n>17时,Tn=Sn-2S17,由等差数列的求和公式得出结果.
解答 解:(1)数列{an}中,a1=-60,an+1=an+4,
∴an+1-an=4,
∴数列{an}是公差为4的等差数列,
∴an=-60+4(n-1)=4n-64;
(2)令an=4n-64≥0,解得n≥16,
∴数列{an}的前15项为负数,第16项为0,从第17项开始为正值,
∴当n≤16时,数列{|an|}的前n项和为
Sn=-Tn=-$\frac{n(-60+4n-64)}{2}$=62n-2n2;
当n>16时,Sn=Tn-2T16=(2n2-62n)-2(2×162-62×16)=2n2-62n+960;
∴Sn=$\left\{\begin{array}{l}{62n-{2n}^{2},n≤16}\\{{2n}^{2}-62n+960,n>16}\end{array}\right.$.
点评 本题考查了等差数列的求和公式,也考查了分类讨论思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$tan35° | D. | tan35° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
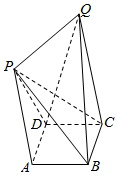 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Q<P<R | B. | P<Q<R | C. | Q<R<P | D. | P<R<Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com