
分析 首先①当N点与C点重合时,线段MN与BD所成的角最大,进一步利用解三角形知识利用余弦定理求出角的余弦值.
②当N点与D点重合时,线段MN与BD所成的角最小,直接在△MBD中,线段MD与BD所成角为30°,求出夹角的余弦值.最后求出角的余弦值的范围.
解答 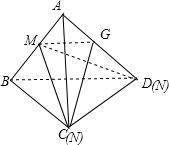 解:在正四面体ABCD中,M是AB的中点,N是棱CD上的一个动点,
解:在正四面体ABCD中,M是AB的中点,N是棱CD上的一个动点,
则:①当N点与C点重合时,线段MN与BD所成的角最大,
设:正四面体的边长为2,
取AD的中点,连接MN、NG,
利用勾股定理得:CM=$\sqrt{4-1}=\sqrt{3}$,
M、G是AB和AD的中点,所以:MG=1,
同理解得:CG=$\sqrt{3}$,
在△CMG中,利用余弦定理得:$cosα=\frac{3+1-3}{2•\sqrt{3}•1}=\frac{\sqrt{3}}{6}$,
即:所成角的余弦值最小为$\frac{\sqrt{3}}{6}$.
②当N点与D点重合时,线段MN与BD所成的角最小,
连接DM,在△MBD中,线段MD与BD所成角为30°,
所以:cos$α=\frac{\sqrt{3}}{2}$,
即所成角的余弦值最大为$\frac{\sqrt{3}}{2}$.
所以:cosα的范围为:[$\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{2}$].
故答案为:[$\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{2}$]
点评 本题考查的知识要点:异面直线的夹角的应用,余弦定理的应用,主要考查学生的应用能力和空间想象能力.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα=-αcosβ | B. | sinα=αcosβ | C. | cosα=βsinβ | D. | sinβ=βsinα |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
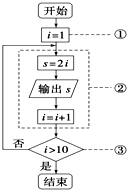
| A. | ①是循环变量初始化,循环就要开始 | |
| B. | ②为循环体 | |
| C. | ③是判断是否继续循环的终止条件 | |
| D. | 输出的S值为2,4,6,8,10,12,14,16,18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com