
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f (x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性;
(3)求出f(x)在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.
解:(1)f(-1)=kf(1)=-k,
∵f(0.5)=kf(2.5),
∴f(2.5)=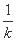 f(0.5)=
f(0.5)= 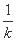 (0.5-2)×0.5=-
(0.5-2)×0.5=- .
.
(2)∵对任意实数x,f(x)=kf(x+2),
∴f(x-2)=kf(x),
∴f(x)=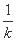 f(x-2),
f(x-2),
当-2≤x<0时,0≤x+2<2,f(x)=kf(x+2)=kx(x+2);
当-3≤x<-2时,-1≤x+2<0,
f(x)=kf(x+2)=k2(x+2)(x+4);
当2<x≤3时,0<x-2≤1,
f(x)=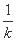 f(x-2)=
f(x-2)=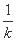 (x-2)(x-4).
(x-2)(x-4).
故f(x)=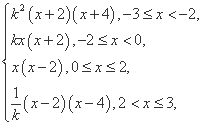
∵k<0,
∴f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1]上为减函数.
(3)由函数f(x)在[-3,3]上的单调性可知,
f(x)在x=-3或x=1处取得最小值f(-3)=-k2或f(1)=-1,
而在x=-1或x=3处取得最大值f(-1)=-k或
f(3)=-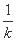 .
.
故有①k<-1时,f(x)在x=-3处取得最小值
f(-3)=-k2,
在x=-1处取得最大值f(-1)=-k.
②k=-1时,f(x)在x=-3与x=1处取得最小值f(-3)=f(1)=-1,
在x=-1与x=3处取得最大值f(-1)=f(3)=1.
③-1<k<0时,f(x)在x=1处取得最小值f(1)=-1,在x=3处取得最大值f(3)=-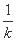 .
.


科目:高中数学 来源: 题型:
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
(A)4 (B)3 (C)2 (D)1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知减函数f(x)的定义域是R,m,n∈R,如果不等式f(m)-f(n)>f(-m)-f(-n)成立,那么在下列给出的四个不等式中,正确的是( )
(A)m+n<0 (B)m+n>0
(C)m-n<0 (D)m-n>0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|log2x|,正实数m、n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m+n等于( )
(A)-1 (B)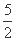 (C)1 (D)2
(C)1 (D)2
查看答案和解析>>
科目:高中数学 来源: 题型:
在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为( )
(A)[0,4] (B)[1,4] (C)[0,8] (D)[1,8]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=4x的焦点为F,过F的直线与该抛物线相交于A(x1,y1)、B(x2,y2)两点,则 +
+ 的最小值是( )
的最小值是( )
(A)4 (B)8 (C)12 (D)16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com