
分析 (1)利用直线l:mx-y+1-m=0恒过过定点P(1,1),可判明在圆内,即可证明直线l和圆C总相交.
(2)直线l与圆C的交点为A,B,若|AB|=$\sqrt{17}$,则圆心到直线的距离d=$\frac{\sqrt{3}}{2}$,求出m,即可求直线的倾斜角;
(3)由已知得到直线过定点P(1,1),设出AB中点M的坐标,分M与P重合和不重合结合直角三角形中的勾股定理得弦AB的中点M的轨迹方程;
(4)把线段的长度比转化为两个想两件的关系,由向量的坐标运算得到A,B两点横坐标间的关系,联立直线与圆的方程化为关于x的一元二次方程,由根与系数关系得到A,B两点横坐标的和,求出其中一点的横坐标,最后再代入关于x的方程得到关于m的方程,求解得到m的值,则直线方程可求.
解答 (1)证明:直线l:mx-y+1-m=0恒过过定点P(1,1),
∵点P(1,1)在圆内,∴直线l和圆C总相交;
(2)解:直线l与圆C的交点为A,B,若|AB|=$\sqrt{17}$,则圆心到直线的距离d=$\frac{\sqrt{3}}{2}$,
∴$\frac{|-m|}{\sqrt{{m}^{2}+1}}$=$\frac{\sqrt{3}}{2}$,
∴m=$±\sqrt{3}$,
∴直线的倾斜角为60°或120°.
(3)解:∵CM⊥MP,
∴弦AB的中点M的轨迹是以CP为直径的圆,方程为(x-$\frac{1}{2}$)2+(y-1)2=$\frac{1}{4}$;
(4)解:设A(x1,y1),B(x2,y2),由$\frac{|AP|}{|PB|}$=$\frac{1}{2}$,得$\overrightarrow{AP}=\frac{1}{2}\overrightarrow{PB}$,
∴1-x1=$\frac{1}{2}$(x2-1),化简的x2=3-2x1…①
又由直线代入圆的方程,消去y得:(1+m2)x2-2m2x+m2-5=0…(*)
∴x1+x2=$\frac{2{m}^{2}}{1+{m}^{2}}$…②
由①②解得x1=$\frac{3+{m}^{2}}{1+{m}^{2}}$,代入(*)式解得m=±1,
∴直线l的方程为x-y=0或x+y-2=0
点评 本题考查了与直线有关的动点的轨迹方程,考查了直线与圆的关系,体现了分类讨论的数学思想方法和数学转化思想方法,考查了学生的灵活处理问题的能力和计算能力,是中高档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
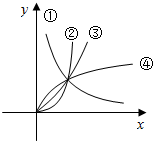 如图表示的是四个幂函数在同一坐标系中第一象限内的图象,则幂函数y=x${\;}^{\frac{1}{2}}$的图象是( )
如图表示的是四个幂函数在同一坐标系中第一象限内的图象,则幂函数y=x${\;}^{\frac{1}{2}}$的图象是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com