
分析 设圆C2上点P,利用直角三角形中的射影定理把AG,PG用PC1表示,从而用PC1表示三角形PAB的面积,由面积为1求出PC1的值,再由PC1的范围列关于m的不等式组求解.
解答 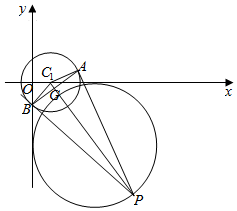 解:如图,由圆C1:(x-1)2+y2=2,圆C2:(x-m)2+(y+m)2=m2,
解:如图,由圆C1:(x-1)2+y2=2,圆C2:(x-m)2+(y+m)2=m2,
得C1(1,0),C2(m,-m),
设圆C2上点P,则PA2=PG•PC1,
而$P{A}^{2}=P{{C}_{1}}^{2}-2$,
∴$P{{C}_{1}}^{2}-2=PG•P{C}_{1}$,则$PG=\frac{P{{C}_{1}}^{2}-2}{P{C}_{1}}$,
$AG=\sqrt{P{A}^{2}-P{G}^{2}}=\sqrt{P{{C}_{1}}^{2}-2-(\frac{P{{C}_{1}}^{2}-2}{P{C}_{1}})^{2}}$=$\frac{\sqrt{2P{{C}_{1}}^{2}-4}}{P{C}_{1}}$,
∴${S}_{△PAB}=2•\frac{1}{2}•\frac{P{{C}_{1}}^{2}-2}{P{C}_{1}}•\frac{\sqrt{2P{{C}_{1}}^{2}-4}}{P{C}_{1}}$=$\frac{(P{{C}_{1}}^{2}-2)\sqrt{2P{{C}_{1}}^{2}-4}}{P{{C}_{1}}^{2}}$=1.
令$\sqrt{2P{{C}_{1}}^{2}-4}=t(t≥0)$,
得t3-t2-4=0,解得:t=2.
即$\sqrt{2P{{C}_{1}}^{2}-4}=2$,∴PC1=2.
圆C2:(x-m)2+(y+m)2=m2上点P到C1距离的最小值为|C1C2|-m=$\sqrt{(m-1)^{2}+(-m)^{2}}$-m,
最大值为|C1C2|+m=$\sqrt{(m-1)^{2}+(-m)^{2}}$+m,
由$\sqrt{(m-1)^{2}+(-m)^{2}}$-m≤2≤$\sqrt{(m-1)^{2}+(-m)^{2}}$+m,
得$\left\{\begin{array}{l}{\sqrt{(m-1)^{2}+{m}^{2}}-m≤2①}\\{\sqrt{(m-1)^{2}+{m}^{2}}+m≥2②}\end{array}\right.$,
解①得:$3-2\sqrt{3}≤m≤3+2\sqrt{3}$,
解②得:m≤-3或m≥1.
取交集得:1$≤m≤3+2\sqrt{3}$.
∴正数m得取值范围是[1,$3+2\sqrt{3}$].
故答案为:[1,$3+2\sqrt{3}$].
点评 本题考查圆的切线方程,考查了圆的切线与圆位置关系的应用,考查数学转化思想方法,考查计算能力,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-3i | B. | -3-i | C. | 3+5i | D. | 5+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
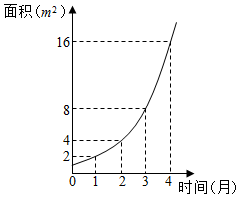 最近几年,每年11月初,黄浦江上漂浮着的水葫芦便会迅速增长,严重影响了市容景观,为了解决这个环境问题,科研人员进行科研攻关,如图是科研人员在实验室池塘中观察水葫芦面积与时间的函数关系图象,假设其函数关系为指数函数,并给出下列说法:
最近几年,每年11月初,黄浦江上漂浮着的水葫芦便会迅速增长,严重影响了市容景观,为了解决这个环境问题,科研人员进行科研攻关,如图是科研人员在实验室池塘中观察水葫芦面积与时间的函数关系图象,假设其函数关系为指数函数,并给出下列说法:| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | ($\frac{1}{2}$,$\frac{9}{4}$] | C. | (1,$\frac{9}{2}$] | D. | ($\frac{1}{2}$,$\frac{5}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac<bc | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a-b}$$>\frac{1}{a}$ | D. | a2<b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{20}{7}$,-$\frac{8}{7}$) | B. | (-∞,-3)∪(-$\frac{8}{7}$,+∞) | C. | (-2,-$\frac{10}{7}$) | D. | (-∞,-2)∪(-$\frac{10}{7}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
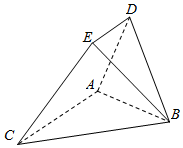 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com