
分析 (1)求出圆心距与半径比较,即可判断两圆的位置关系;
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,即可得出结论.
解答 解:(1)圆C1的圆心C1(-3,1),半径r1=2;
圆C2的圆心C2(4,5),半径r2=2.
∴C1C2═$\sqrt{(4+3)^{2}+(5-1)^{2}}$=$\sqrt{65}$>r1+r2=4,∴两圆相离;
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,
连心线所在直线方程为:$\frac{y-1}{5-1}=\frac{x+3}{4+3}$,即4x-7y+19=0.
点评 本题考查圆与圆的位置关系,考查直线方程,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 空间中两组对边分别相等的四边形为平行四边形 | |
| B. | 所有梯形都有外接圆 | |
| C. | 所有的质数的平方都不是偶数 | |
| D. | 不存在一个奇数,它的立方是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{9}{2}$ | D. | -$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
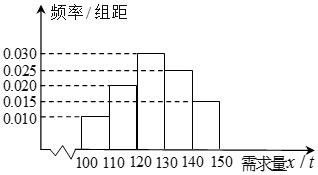 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x≠0,则x2-3x≠0”的否命题是“若x=0,则x2-3x=0” | |
| B. | 命题“?x∈R,lg(x2-x+1)≥0”是假命题 | |
| C. | 命题“?x∈R,3sinx=$\sqrt{3}$”是真命题 | |
| D. | 命题“若x=1,则向量$\overrightarrow{a}$=(-2x,1)与$\overrightarrow{b}$=(-2,x)共线”的逆命题是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com