
分析 先根据两个截面圆的面积分别求出对应圆的半径,再分析出两个截面所存在的两种情况,最后对每一种情况分别求出两个平行平面的距离即可.
解答 解:设两个截面圆的半径别为r1,r2.球心到截面的距离分别为d1,d2.球的半径为R.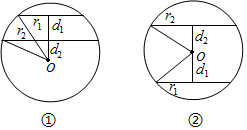
由πr12=49π,得r1=7.
由πr22=400π,得r2=20.
如图①所示.当球的球心在两个平行平面的外侧时,这两个平面间的距离为球心与两个截面圆的距离之差,
即d1-d2=$\sqrt{2{5}^{2}-{7}^{2}}-\sqrt{2{5}^{2}-2{0}^{2}}=9$.
如图②所示.当球的球心在两个平行平面的之间时,这两个平面间的距离为球心与两个截面圆的距离之和.
即d1+d2=$\sqrt{2{5}^{2}-{7}^{2}}+\sqrt{2{5}^{2}-2{0}^{2}}=39$.
故答案为:9或39.
点评 本题主要考查两个平行平面间的距离计算问题.此题重点考查球中截面圆半径,球半径之间的关系以及空间想象能力和计算能力.本题的易错点在于只考虑一种情况,从而漏解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,9] | C. | [1,9] | D. | [9,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com