
分析 (1)利用已知条件直接代入|f(0)|≤1,|f(1)|≤1,求出a,b的范围,然后利用绝对值的性质证明即可.
(2)利用条件以及(1)的结果,讨论a的范围求解函数的最值得到方程,求出a的值.
解答 (1)证:∵|f(0)|=|a|≤1;
|f(1)|=|b|≤1;
∴|f(x)|=|a(x2-1)+bx|≤|a||x2-1|+|b||x|≤|x2-1|+|x|,
∵-1≤x≤1,
∴|f(x)|≤|x2-1|+|x|=1-x2+|x|=-(|x|-$\frac{1}{2}$)2+$\frac{5}{4}$,
∴$|{f(x)}|≤\frac{5}{4}$.
(2)解:b=1当|a|≤1时,∵$f(x)≤\frac{5}{4}$,f(x)的最大值为$\frac{17}{8}$矛盾,∴|a|>1
当a>1时,∵$\frac{-1}{2a}∈(-1.0)$,∴f(x)在$(-1,-\frac{1}{2a})$是减函数,$(-\frac{1}{2a},1)$是增函数,
∵f(1)=1,f(-1)=-1,
∴f(x)max=f(1)=1不符题意.
当a<-1时 $-\frac{1}{2a}(-10,1)$,∴f(x)在$(-1,-\frac{1}{2a})$是增函数,
在$(-\frac{1}{2a},1)$是减函数,
∴$f{(x)_{max}}=f(-\frac{1}{2a})=-a-\frac{1}{4a}=\frac{17}{8}$-8a2-2=17a,即8a2+17a+2=0,
∴$a=-\frac{1}{8}$或a=-2,
∵a<-1,
∴a=-2.
点评 本题考查函绝对值的函数的应用,函数的最值的求法,考查分类讨论思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-1或a>1 | B. | a≤-1或a≥1 | C. | a≥1 | D. | a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
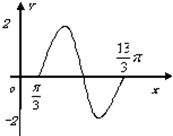 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<$\frac{π}{2}$)一段图象如图所示.
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<$\frac{π}{2}$)一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com