
已知某地区中小学生人数和近视情况如下表所示:
年级 | 人数 | 近视率 |
小学 | 3500 | 10% |
初中 | 4500 | 30% |
高中 | 2000 | 50% |
为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,
则:(Ⅰ)样本容量为___________;(Ⅱ)抽取的高中生中,近视人数为___________.
科目:高中数学 来源:2014-2015学年河北省高一12月月考数学试卷(解析版) 题型:解答题
(12分)正方形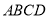 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△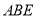 是等腰直角三角形,
是等腰直角三角形,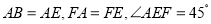
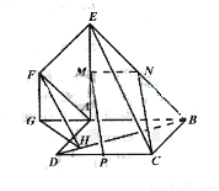
(1)求证: ;
;
(2)设线段 的中点为
的中点为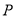 ,在直线
,在直线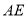 上是否存在一点
上是否存在一点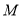 ,使得
,使得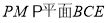 ?若存在,请指出点
?若存在,请指出点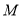 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高三教学质量统一检测一理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图1,在Rt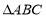 中,
中,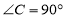 ,
,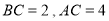 .
.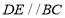 ,将
,将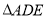 沿
沿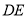 折起到
折起到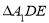 的位置,使
的位置,使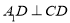 ,如图2.
,如图2.

(Ⅰ)求证: 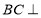 平面
平面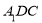 ;
;
(Ⅱ)若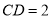 ,求平面
,求平面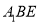 与平面
与平面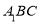 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试文科数学试卷(解析版) 题型:填空题
给出以下数对序列:
(1,1)
(1,2) (2,1)
(1,3) (2,2) (3,1)
(1,4) (2,3) (3,2) (4,1)
记第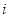 行的第
行的第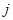 个数对为
个数对为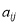 ,如
,如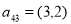 ,则
,则
(Ⅰ)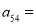 ________;(Ⅱ)
________;(Ⅱ)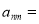 ________.
________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试文科数学试卷(解析版) 题型:选择题
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面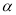 上.用一平行于平面
上.用一平行于平面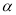 的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为
的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为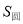 和
和 ,那么
,那么
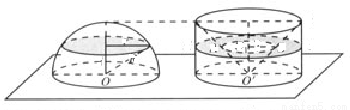
A.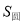
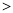
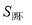 B.
B.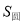 =
=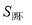 C.
C.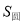
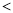
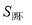 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知椭圆C: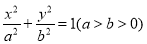 的焦距为4,其长轴长和短轴长之比为
的焦距为4,其长轴长和短轴长之比为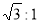 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F为椭圆C的右焦点,T为直线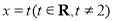 上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求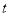 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当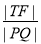 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试理科数学试卷(解析版) 题型:选择题
根据如下样本数据
x | 3 | 4 | 5 | 6 | 7 |
y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为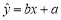 .若
.若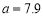 ,则
,则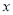 每增加1个单位,
每增加1个单位,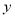 就
就
A.增加 个单位 B.减少
个单位 B.减少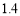 个单位
个单位
C.增加 个单位 D.减少
个单位 D.减少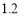 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三上学期期末质量检测理科数学试卷(解析版) 题型:选择题
已知抛掷一枚质地均匀的硬币,正面朝上的概率为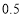 .现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
.现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
101 111 010 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( ).
A.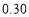 B.
B.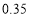 C.
C.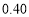 D.
D.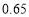
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com