
���� ����֪������������$\overrightarrow c$��$\overrightarrow a$�ļнǵ���$\overrightarrow c$��$\overrightarrow b$�ļн���ʽ���mֵ��
��� �⣺��$\overrightarrow a=��1��2��$��$\overrightarrow b=��6��3��$����$\overrightarrow c=m\overrightarrow a+\overrightarrow b$=��m+6��2m+3����
��$|\overrightarrow{a}|=\sqrt{5}$��$|\overrightarrow{b}|=3\sqrt{5}$��$|\overrightarrow{c}|=\sqrt{��m+6��^{2}+��2m+3��^{2}}$��
$\overrightarrow{c}•\overrightarrow{a}$=5m+12��$\overrightarrow{c}•\overrightarrow{b}$=12m+45��
��$\overrightarrow c$��$\overrightarrow a$�ļнǵ���$\overrightarrow c$��$\overrightarrow b$�ļнǣ�
��$\frac{5m+12}{\sqrt{5}|\overrightarrow{c}|}=\frac{12m+45}{3\sqrt{5}|\overrightarrow{c}|}$����ã�m=3��
�ʴ�Ϊ��3��
���� ���⿼��ƽ�����������������㣬�������������������ļнǣ����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $2\sqrt{3}$ | C�� | 4 | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
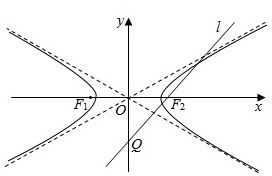 ��ͼ��˫���ߦ���$\frac{{x}^{2}}{3}$-y2=1�����ҽ���ֱ�ΪF1��F2����F2��ֱ��l��y���ڵ�Q��
��ͼ��˫���ߦ���$\frac{{x}^{2}}{3}$-y2=1�����ҽ���ֱ�ΪF1��F2����F2��ֱ��l��y���ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��4] | B�� | [4��+�ޣ� | C�� | ��0��2] | D�� | [2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������ABCD�У�AD��BC����ABC=90�㣬AB=a��AD=3a���ҡ�ADC=arcsin$\frac{{\sqrt{5}}}{5}$��PA��ƽ��ABCD��PA=a��������P-CD-A�Ĵ�СΪarctan$\frac{\sqrt{5}}{3}$��
������ABCD�У�AD��BC����ABC=90�㣬AB=a��AD=3a���ҡ�ADC=arcsin$\frac{{\sqrt{5}}}{5}$��PA��ƽ��ABCD��PA=a��������P-CD-A�Ĵ�СΪarctan$\frac{\sqrt{5}}{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com