
分析 易得直线恒过定点C(1,-1),圆x2+y2=4圆心为(0,0)半径为2,$\overrightarrow{AO}$$•\overrightarrow{AB}$=4-2×2×cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>,可得当AB⊥OC时,式子取最小值,数形结合联立方程组解点的坐标可得.
解答 解:直线ax+y-a+1=0可化为y+1=-a(x-1),
恒过定点C(1,-1),圆x2+y2=4圆心为(0,0)半径为2,
∴$\overrightarrow{AO}$$•\overrightarrow{AB}$=$\overrightarrow{OA}$•$\overrightarrow{BA}$=$\overrightarrow{OA}$•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=${\overrightarrow{OA}}^{2}$-$\overrightarrow{OA}$•$\overrightarrow{OB}$
=4-2×2×cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>,
当AB⊥OC时,<$\overrightarrow{OA}$,$\overrightarrow{OB}$>最小,cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>取最大值,
此时$\overrightarrow{AO}$$•\overrightarrow{AB}$=4-4cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>取最小值,
此时OC的斜率为-1,由垂直关系可得-a=1,解得a=-1,
故此时直线方程为y+1=x-1,即y=x-2,
联立$\left\{\begin{array}{l}{y=x-2}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$可解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,
∴<$\overrightarrow{OA}$,$\overrightarrow{OB}$>取最小值$\frac{π}{2}$,cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>取最大值0,
此时$\overrightarrow{AO}$$•\overrightarrow{AB}$=4-4cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>取最小值4,
故答案为:4
点评 本题考查直线和圆相交的性质,涉及向量的数量积的最值和三角函数,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
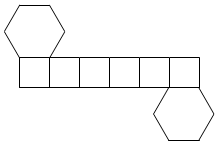 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{5}{4}$) | B. | ($\frac{5}{4}$,+∞) | C. | (1,+∞) | D. | (-∞,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
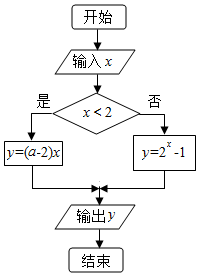
| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{51}{70}$ | B. | $\frac{70}{51}$ | C. | $\frac{35}{17}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com