
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
分析 由|AB|=4a的直线1恰好有3条,由双曲线的对称性可得,必有一条与x轴垂直,另两条关于x轴对称,令x=c,代入双曲线方程,计算即可得到弦长,由渐近线方程即可得到所求.
解答 解:由|AB|=4a的直线1恰好有3条,
由双曲线的对称性可得,必有一条与x轴垂直,
另两条关于x轴对称,
令x=c,代入双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),可得
y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,
即有此时|AB|=$\frac{2{b}^{2}}{a}$=4a,
即为b=$\sqrt{2}$a,
即有双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\sqrt{2}$x.
故选:A.
点评 本题考查双曲线的渐近线方程的求法,注意运用双曲线的对称性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [0,4$\sqrt{2}$] | B. | [2,4] | C. | [2$\sqrt{2}$,4$\sqrt{2}$] | D. | [2$\sqrt{2}$,3$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于( )

A. B.
B. C.
C.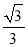 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com