
分析 如图所示,分别取AC,A1C1的中点O,O1,连接OO1,取OE=1,连接DE,B1O1,AE.利用等边三角形的性质与直棱柱的性质可得:BO⊥侧面ACC1A1.四边形BODE是矩形.DE⊥侧面ACC1A1.因此∠DAE是AD与平面AA1C1C所成的角,为α,再利用直角三角形的边角关系即可得出.
解答 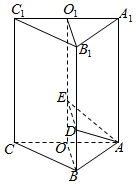 解:如图所示,
解:如图所示,
分别取AC,A1C1的中点O,O1,连接OO1,取OE=1,连接DE,B1O1,AE.
∴BO⊥AC,
∵侧棱AA1⊥底面ABC,∴三棱柱ABC-A1B1C1是直棱柱.
由直棱柱的性质可得:BO⊥侧面ACC1A1.
∴四边形BODE是矩形.
∴DE⊥侧面ACC1A1.
∴∠DAE是AD与平面AA1C1C所成的角,为α,
∴DE=$\frac{\sqrt{3}}{2}$=OB.
AD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
在Rt△ADE中,sinα=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{2}}$=$\frac{\sqrt{6}}{4}$.
故答案为:$\frac{\sqrt{6}}{4}$.
点评 本题考查了直棱柱的性质、空间角、空间位置关系、等边三角形的性质,考查了推理能力与计算能力,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:选择题
| A. | ?n∈N*,anan+1≤an+2 | B. | ?n∈N*,an+an+2=2an+1 | ||
| C. | ?n∈N*,Sn<an+1 | D. | ?n∈N*,an+an+3=an+1+an+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-3y=0 | B. | $\sqrt{3}$x-y=0 | C. | x-$\sqrt{3}$y=0 | D. | 3x-y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
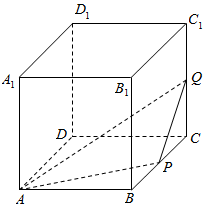 正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)
正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com