
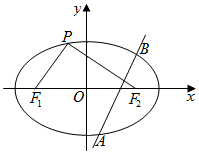
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.分析 解法一:(Ⅰ)由已知有${({S_{△P{F_1}{F_2}}})_{max}}=\frac{1}{2}×2c×b=bc=2$,$e=\frac{{\sqrt{2}}}{2}⇒a=\sqrt{2}c$,又a2=b2+c2,联立解出即可得出.
(Ⅱ)设点A(x1,y1),B(x2,y2),AB的中点为H(x0,y0),把直线方程与椭圆方程联立可得根与系数的关系,利用弦长公式可得|AB|,比较$\frac{|AB{|}^{2}}{4}$与|MH|2即可得出.
解法二:(II)利用数量积运算性质、向量夹角公式可得∠AMB为锐角,即可得出位置关系.
解答 解法一:(Ⅰ)由已知有${({S_{△P{F_1}{F_2}}})_{max}}=\frac{1}{2}×2c×b=bc=2$,…(1分)
∵$e=\frac{{\sqrt{2}}}{2}⇒a=\sqrt{2}c$,又a2=b2+c2,∴$b=c=\sqrt{2}$,∴a=2,…(3分)
∴椭圆E的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$; …(4分)
(Ⅱ)设点A(x1,y1),B(x2,y2),AB的中点为H(x0,y0),
由$\left\{\begin{array}{l}x=my+1\\{x^2}+2{y^2}=4\end{array}\right.⇒({m^2}+2){y^2}+2my-3=0$,…(5分)
∴${y_1}+{y_2}=\frac{-2m}{{{m^2}+2}}$,${y_1}{y_2}=\frac{-3}{{{m^2}+2}}$,∴${y_0}=\frac{-m}{{{m^2}+2}}$,…(6分)
∴${|{MH}|^2}={({x_0}-3)^2}+y_0^2={(m{y_0}-2)^2}+y_0^2=({m^2}+1)y_0^2-4m{y_0}+4$,…(7分)
$\frac{{{{|{AB}|}^2}}}{4}=\frac{{{{({x_1}-{x_2})}^2}+{{({y_1}-{y_2})}^2}}}{4}=\frac{{(1+{m^2}){{({y_1}-{y_2})}^2}}}{4}=\frac{{(1+{m^2})[{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}]}}{4}$=$(1+{m^2})(y_0^2-{y_1}{y_2})$,…(9分)
∴$|MH{|}^{2}-\frac{|AB{|}^{2}}{4}$=-4my0+4(1+m2)y1y2=$\frac{4{m}^{2}}{{m}^{2}+2}$+4+$\frac{-12(1+{m}^{2})}{{m}^{2}+2}$=$\frac{5({m}^{2}+1)}{{m}^{2}+2}$>0,
∴$|{MH}|>\frac{{|{AB}|}}{2}$,
因此,点M(3,0)在以线段AB为直径的圆外.…(12分)
解法二:(Ⅰ)同解法一;(Ⅱ)设点A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}x=my+1\\{x^2}+2{y^2}=4\end{array}\right.⇒({m^2}+2){y^2}+2my-3=0$,∴${y_1}+{y_2}=\frac{-2m}{{{m^2}+2}}$,${y_1}{y_2}=\frac{-3}{{{m^2}+2}}$,
…(6分)
∵$\overrightarrow{MA}=({x_1}-3,{y_1})$,$\overrightarrow{MB}=({x_2}-3,{y_2})$,
∴$\overrightarrow{MA}•\overrightarrow{MB}$=(x1-3,y1)•(x2-3,y2)=(m2+1)y1y2-2m(y1+y2)+4=$\frac{-3({m}^{2}+1)}{{m}^{2}+2}$+$\frac{4{m}^{2}}{{m}^{2}+2}$+4=$\frac{5({m}^{2}+1)}{{m}^{2}+2}$>0,(10分)
∴$cos<\overrightarrow{MA},\overrightarrow{MB})>0$,又$\overrightarrow{MA},\overrightarrow{MB}$不共线,∴∠AMB为锐角,…(11分)
因此,点M(3,0)在以AB为直径的圆外. …(12分)
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、弦长公式、三角形面积计算公式、向量数量积运算性质、向量夹角公式、点与圆的位置关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | 3 | C. | $-\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
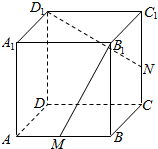 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:| A. | ① | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [3,+∞) | C. | [1,3] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com