
| A. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
分析 由椭圆的定义及对称性求得丨AF丨+丨BF丨=2a,利用直角三角形的性质求得丨AF丨及丨BF丨,利用椭圆的离心率公式及正弦函数的图象及性质,即可求得e的取值范围.
解答 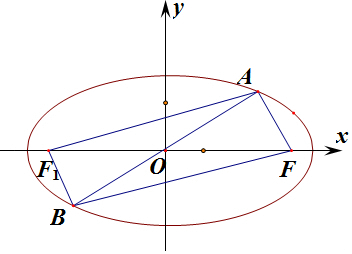 解:由已知,点B和点A关于原点对称,则点B也在椭圆上,
解:由已知,点B和点A关于原点对称,则点B也在椭圆上,
设椭圆的左焦点为F1,则根据椭圆定义:丨AF丨+丨AF1丨=2a=10,
根据椭圆对称性可知:丨AF1丨=丨BF丨,因此丨AF丨+丨BF丨=2a=10①;
因为AF⊥BF,则在Rt△ABF中,O为斜边AB中点,则丨AB丨=2丨OF丨=2c,那么丨AF丨=2csinα②,丨BF丨=2ccosα③;
将②、③代入①得,2csinα+2ccosα=2a,
则离心率e=$\frac{c}{a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$,
由α∈[$\frac{π}{6}$,$\frac{π}{4}$],α+$\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{π}{2}$],
由sin$\frac{5π}{12}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
由函数的单调性可知:sin(α+$\frac{π}{4}$)∈[$\frac{\sqrt{6}+\sqrt{2}}{4}$,1],则e∈[$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1],
故选:C.
点评 本题考查椭圆的定义,三角函数关系式的恒等变换,利用定义域求三角函数的值域,离心率公式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1≤0 | D. | ?x∈R,x3-x2+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了一项$\frac{1}{2(k+1)}$ | |
| B. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | |
| C. | 增加了一项$\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ | |
| D. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
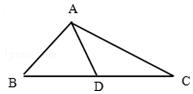 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-1,0,1,2} | C. | [-2,2] | D. | {0,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com