
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
分析 利用三角函数的辅助角公式求出$cos(x+\frac{π}{3})+\sqrt{3}sin(x+\frac{π}{3})≥1$的等价条件,利用几何概型的概率公式即可得到结论.
解答 解:由$cos(x+\frac{π}{3})+\sqrt{3}sin(x+\frac{π}{3})≥1$得2sin(x+$\frac{π}{2}$)≥1,
即cosx≥$\frac{1}{2}$,
∵0≤x≤2π,
∴x的取值范围是0≤x≤$\frac{π}{3}$或$\frac{5π}{3}$≤x≤2π,
则“$cos(x+\frac{π}{3})+\sqrt{3}sin(x+\frac{π}{3})≥1$”发生的概率P=$\frac{\frac{2π}{3}}{2π}$=$\frac{1}{3}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,利用辅助角公式求出不等式的等价条件是解决本题的关键.


科目:高中数学 来源: 题型:解答题
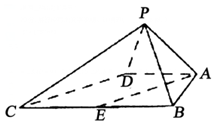 如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 34种 | B. | 48种 | C. | 96种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.6 | C. | 0.7 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {-1,2} | C. | $\{0,\frac{1}{2}\}$ | D. | $\{\frac{1}{2},2\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x±2\sqrt{2}y=0$ | B. | $2\sqrt{2}x±y=0$ | C. | x±8y=0 | D. | 8x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com