
分析 (1)根据题意可知cos(x+a)=cos(-x)=cosx,故而a=2kπ,k∈Z;
(2)由新定义可推出f(x)为偶函数,从而求出f(x)在[0,1]上的解析式,讨论m与[0,1]的关系判断f(x)的单调性得出f(x)的最值;
(3)根据新定义可知g(x)为周期为2的偶函数,作出g(x)的函数图象,根据函数图象得出p的值.
解答 解:(1)假设y=cosx具有“P(a)性质”,则cos(x+a)=cos(-x)=cosx恒成立,
∵cos(x+2kπ)=cosx,
∴函数y=cosx具有“P(a)性质”,且所有a的值的集合为{a|a=2kπ,k∈Z}.
(2)因为函数y=f(x)具有“P(0)性质”,所以f(x)=f(-x)恒成立,
∴y=f(x)是偶函数.
设0≤x≤1,则-x≤0,∴f(x)=f(-x)=(-x+m)2=(x-m)2.
①当m≤0时,函数y=f(x)在[0,1]上递增,值域为[m2,(1-m)2].
②当$0<m<\frac{1}{2}$时,函数y=f(x)在[0,m]上递减,在[m,1]上递增,
ymin=f(m)=0,${y_{max}}=f(1)={(1-m)^2}$,值域为[0,(1-m)2].
③当$\frac{1}{2}≤m≤1$时,ymin=f(m)=0,${y_{max}}=f(0)={m^2}$,值域为[0,m2].
④m>1时,函数y=f(x)在[0,1]上递减,值域为[(1-m)2,m2].
(3)∵y=g(x)既具有“P(0)性质”,即g(x)=g(-x),∴函数y=g(x)偶函数,
又y=g(x)既具有“P(2)性质”,即g(x+2)=g(-x)=g(x),
∴函数y=g(x)是以2为周期的函数.
作出函数y=g(x)的图象如图所示:
由图象可知,当p=0时,函数y=g(x)与直线y=px交于点(2k,0)(k∈Z),即有无数个交点,不合题意.
当p>0时,在区间[0,2016]上,函数y=g(x)有1008个周期,要使函数y=g(x)的图象与直线y=px有2017个交点,
则直线在每个周期内都有2个交点,且第2017个交点恰好为(2017,1),所以$p=\frac{1}{2017}$.
同理,当p<0时,$p=-\frac{1}{2017}$.
综上,$p=±\frac{1}{2017}$.
点评 本题考查了对新定义的理解,函数单调性与周期性的应用,二次函数的性质,函数图象的意义,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
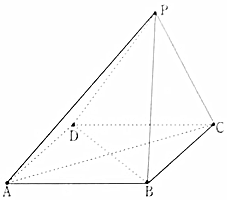 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com