
分析 根据题意,分析可得需要将1、2、3、4、5、6分成3组,其中1和2,3和4,5和6必须在一组,进而分2步进行分析:首先分析每种2个数之间的顺序,再将分好的三组对应三个绝对值,最后由分步计数原理计算可得答案.
解答 解:根据题意,若|a1-a2|+|a3-a4|+|a5-a6|=3,则|a1-a2|=|a3-a4|=|a5-a6|=1,
需要将1、2、3、4、5、6分成3组,其中1和2,3和4,5和6必须在一组,
每组2个数,考虑其顺序,有A22种情况,三组共有A22×A22×A22=8种顺序,
将三组全排列,对应三个绝对值,有A33=6种情况,
则不同排列的个数为8×6=48;
故答案为:48.
点评 本题考查排列、组合的应用,注意分析1、2、3、4、5、6如何排列时,能满足|a1-a2|+|a3-a4|+|a5-a6|=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
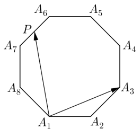 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )| A. | $[0,8+6\sqrt{2}]$ | B. | $[-2\sqrt{2},8+6\sqrt{2}]$ | C. | $[-8-6\sqrt{2},2\sqrt{2}]$ | D. | $[-8-6\sqrt{2},8+6\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $-\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2 | B. | ln2+1 | C. | 1 | D. | $\frac{{{e^2}-1}}{{4{e^2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com