
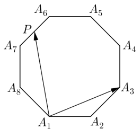
 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )| A. | $[0,8+6\sqrt{2}]$ | B. | $[-2\sqrt{2},8+6\sqrt{2}]$ | C. | $[-8-6\sqrt{2},2\sqrt{2}]$ | D. | $[-8-6\sqrt{2},8+6\sqrt{2}]$ |
分析 由题意求出以A1为起点,以其它顶点为向量的模,再由正弦函数的单调性及值域可得当P与A8重合时,$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$取最小值,求出最小值,结合选项得答案.
解答 解:由题意,正八边形A1A2A3A4A5A6A7A8的每一个内角为135°,
且$|\overrightarrow{{A}_{1}{A}_{2}}|=|\overrightarrow{{A}_{1}{A}_{8}}|=2$,$|\overrightarrow{{A}_{1}{A}_{3}}|=|\overrightarrow{{A}_{1}{A}_{7}}|=2\sqrt{2+\sqrt{2}}$,$|\overrightarrow{{A}_{1}{A}_{4}}|=|\overrightarrow{{A}_{1}{A}_{6}}|=2+\sqrt{2}$,$|\overrightarrow{{A}_{1}{A}_{5}}|=\sqrt{4+2\sqrt{2}}$.
再由正弦函数的单调性及值域可得,
当P与A8重合时,$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$最小为$2×2\sqrt{2+\sqrt{2}}×cos112.5°$=$2×2\sqrt{2+\sqrt{2}}×(-\frac{\sqrt{2-\sqrt{2}}}{2})$=$-2\sqrt{2}$.
结合选项可得$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为$[-2\sqrt{2},8+6\sqrt{2}]$.
故选:B.
点评 本题考查平面向量的数量积运算,考查数形结合的解题思想方法,属中档题.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $({1,\sqrt{2}})$ | D. | $({0,\sqrt{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b的值分别为84,48,则输出的a的值为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b的值分别为84,48,则输出的a的值为( )| A. | 8 | B. | 12 | C. | 24 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com