
分析 (1)a1=1;由于11或2满足各数位上的数字之和为2,可得a2=2;以此类推即可得出a3=3,a4=5.
(2)设满足条件的自然数X的首位为1或2两种情况:当X的首位为1时,则其余各位数字之和为n+1,因此首位为1的自然数X的各位数字之和为n+2的自然数的个数为an+1;当X的首位为2时,则其余各位数字之和为n,因此首位为2的自然数X的各位数字之和为n+2的自然数的个数为an.可得各数位上的数字之和为n+2的自然数个数为an+1+an.即an+2=an+1+an.利用数学归纳法证明:a5n-1(n∈N*)是5的倍数即可.
解答 (1)解:a1=1;
由于11或2满足各数位上的数字之和为2,∴a2=2;
由于111,12,21满足各数位上的数字之和为3,∴a3=3;
由于1111,121,211,112,22满足各数位上的数字之和为4,∴a4=5.
(2)证明:设满足条件的自然数X的首位为1或2两种情况:
当X的首位为1时,则其余各位数字之和为n+1,因此首位为1的自然数X的各位数字之和为n+2的自然数的个数为an+1;
当X的首位为2时,则其余各位数字之和为n,因此首位为2的自然数X的各位数字之和为n+2的自然数的个数为an.
∴各数位上的数字之和为n+2的自然数个数为an+1+an.即an+2=an+1+an.
下面利用数学归纳法证明:a5n-1(n∈N*)是5的倍数.
(i)当n=1时,a4=5,因此是5的倍数;
(ii)假设当n=k(k∈N*)时,a5k-1是5的倍数.
则n=k+1时,a5k+4=a5k+3+a5k+2=2a5k+2+a5k+1=2(a5k+1+a5k)+a5k+1=3a5k+1+2a5k=3(a5k+a5k-1)+2a5k=5a5k+3a5k-1.
而5a5k与a5k-1都是5的倍数,因此a5k+4是5的倍数,
∴则n=k+1时命题成立.
综上可得:命题对于?n∈N*都成立.
点评 本题考查了整除的理论、数学归纳法、类比推理,考查了变形能力,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=logax | B. | y=x3+x | C. | y=3x | D. | y=-$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14:3 | B. | 19:4 | C. | 24:5 | D. | 29:6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
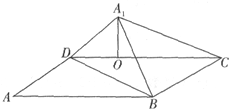 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com