练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数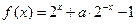(a为实数)．⑴若a<0，用函数单调性定义证明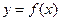：在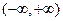上是增函数;⑵若a＝0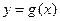，的图象与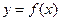的图象关于直线y＝x对称，求函数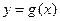的解析式．

    解： (1)设任意实数x1<x2，则f(x1)－ f(x2)＝
    ＝＝  
    ．
    又，∴f(x1)－ f(x2)<0，所以f(x)是增函数．   
    (2)当a＝0时，y＝f(x)＝2x－1，∴2x＝y＋1，∴x＝log2(y＋1)，
    y＝g(x)＝ log2(x＋1)．                   

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数．
    (1)求函数的单调区间，并指出其增减性；
    (2)若关于x的方程至少有三个不相等的实数根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数满足
    (1)求函数的解析式 ;  
    (2)若在上恒成立，求实数的取值范围；
    (3)求当（＞0）时的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）已知函数f(x)=
    (1)若函数定义域为[3,4]，求函数值域
    (2)若函数定义域为[-3,4]，求函数值域

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题满分12分) 已知的反函数为，.
    (1)若，求的取值范围D；
    (2)设函数，当时，求函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）已知是定义在上的奇函数，且，若时，有.
    （1）解不等式；
    (2)若对所有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）
    用总长14.8m的钢条做一个长方体容器的框架，如果所做容器的底面的一边长比另一边长多0.5m，那么高是多少时容器的容积最大？并求出它的最大容积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    求函数在区间[2,6]上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题10分）
    函数f(x)=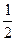(a x+a -x),  (a>0且a≠1)
    (1) 讨论f(x)的奇偶性
    (2) 若函数f(x)的图象经过点(2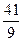，), 求f(x)

    查看答案和解析>>

    同步练习册答案