Question

16．在△ABC中，AB=3，AC=4，BC=5．若I为△ABC的内心，则$\overrightarrow{CI}$•$\overrightarrow{CB}$的值为（　　）

• A． 6
• B． 10
• C． 12
• D． 15

Answer 1

分析 由题意可得，∠A=$\frac{π}{2}$，cosC=$\frac{4}{5}$，利用二倍角的余弦公式求得cos∠ICB的值．用面积法求得三角形的内切圆半径r，再利用直角三角形中的边角关系求得CI的值，可得$\overrightarrow{CI}$•$\overrightarrow{CB}$=|$\overrightarrow{CI}$|•|$\overrightarrow{CB}$|•cos∠ICB 的值．

解答 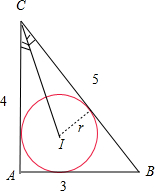解：由题意可得，∠A=$\frac{π}{2}$，cosC=$\frac{AC}{BC}$=$\frac{4}{5}$，
且I为三角形ABC三内角平分线的交点，
∴∠ICB=$\frac{1}{2}$∠C，∴cosC=$\frac{4}{5}$=2cos²∠ICB-1，求得cos∠ICB=$\frac{3\sqrt{10}}{10}$．
设内切圆的半径为r，由S_△ABC=$\frac{1}{2}$AB•AC=6=$\frac{1}{2}$•（AB+AC+BC）r=$\frac{1}{2}$×12×r，
求得r=1．
再根据sin∠ICB=$\frac{\sqrt{10}}{10}$=$\frac{r}{CI}$=$\frac{1}{CI}$，∴CI=$\sqrt{10}$．
∴$\overrightarrow{CI}$•$\overrightarrow{CB}$=|$\overrightarrow{CI}$|•|$\overrightarrow{CB}$|•cos∠ICB=$\sqrt{10}$•5•$\frac{3\sqrt{10}}{10}$=15，
故选：D．

点评 本题主要考查直角三角形中的边角关系，二倍角的余弦公式，两个向量的数量积的定义，属于中档题．