
分析 (1)由椭圆过点P(1,$\frac{3}{2}$),离心率为$\frac{1}{2}$,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)①设直线l的方程为x=my+1,代入椭圆,得(3m2+4)y2+6my-9=0,由此利用根的判别式、韦达定理,结合已知条件能求出t的最大值.
②设直线l的方程为y=$\frac{\sqrt{3}}{2}x+n$,代入椭圆,得$3{x}^{2}+2\sqrt{3}nx+2{n}^{2}-6=0$,由此利用根的判别式、韦达定理,结合已知条件能求出OA2+OB2为定值.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(1,$\frac{3}{2}$),离心率为$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\\{e=\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{1}{2}}\end{array}\right.$,
解得a=2,b=$\sqrt{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)①设直线l的方程为x=my+1,直线l与椭圆C的交点为A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3m2+4)y2+6my-9=0,
△=36m2+36(3m2+4)>0,
${y}_{1}+{y}_{2}=-\frac{6m}{3{m}^{2}+4}$,${y}_{1}{y}_{2}=-\frac{9}{3{m}^{2}+4}$,
∴kAP•kBP=$\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}•\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$=$\frac{{y}_{1}-\frac{3}{2}}{m{y}_{1}}•\frac{{y}_{2}-\frac{3}{2}}{m{y}_{2}}$=$\frac{1}{{m}^{2}}•\frac{{y}_{1}{y}_{2}-\frac{3}{2}({y}_{1}+{y}_{2})+\frac{9}{4}}{{y}_{1}{y}_{2}}$=-$\frac{1}{m}-\frac{3}{4}$,
∴t=kAB•kAP•kBP=-$\frac{1}{{m}^{2}}-\frac{3}{4m}$=-($\frac{1}{m}+\frac{3}{8}$)2+$\frac{9}{64}$,
∴当m=-$\frac{8}{3}$时,t有最大值$\frac{9}{64}$.
②设直线l的方程为y=$\frac{\sqrt{3}}{2}x+n$,直线l与椭圆C的交点为A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=\frac{\sqrt{3}}{2}x+n}\end{array}\right.$,得$3{x}^{2}+2\sqrt{3}nx+2{n}^{2}-6=0$,
$△=(2\sqrt{3}n)^{2}-4×3(2{n}^{2}-6)>0$,
即$-\sqrt{6}<n<\sqrt{6}$,
${x}_{1}+{x}_{2}=-\frac{2\sqrt{3}n}{3}$,${x}_{1}{x}_{2}=\frac{2{n}^{2}-6}{3}$,
$O{A}^{2}+O{B}^{2}={{x}_{1}}^{2}+{{y}_{1}}^{2}+{{x}_{2}}^{2}+{{y}_{2}}^{2}$
=${{x}_{1}}^{2}+{{x}_{2}}^{2}+$($\frac{\sqrt{3}}{2}{x}_{1}$+n)2+($\frac{\sqrt{3}}{2}{x}_{2}$+n)2
=$\frac{7}{4}({{x}_{1}}^{2}+{{x}_{2}}^{2})+\sqrt{3}n({x}_{1}+{x}_{2})+2{n}^{2}$
=$\frac{7}{4}({x}_{1}+{x}_{2})^{2}-\frac{7}{2}{x}_{1}{x}_{2}+\sqrt{3}n({x}_{1}+{x}_{2})+2{n}^{2}$
=$\frac{7}{4}({x}_{1}+{x}_{2})^{2}-\frac{7}{2}{x}_{1}{x}_{2}+\sqrt{3}n$(x1+x2)+2n2
=$\frac{7}{4}(-\frac{2\sqrt{3}}{3}n)^{2}-\frac{7}{2}(\frac{2{n}^{2}-6}{3})+\sqrt{3}n$$(-\frac{2\sqrt{3}}{3}n)+2{n}^{2}$=7.
∴OA2+OB2为定值7.
点评 本题考查椭圆方程的求法,考查实数的最大值的求法,考查代数式的值是否为定值的判断与求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、椭圆性质的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
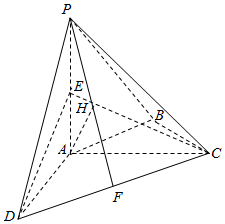 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
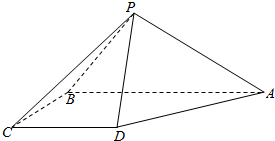 如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.
如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com