
分析 根据数列的定义可判断(1);根据正弦定理可判断(2);根据诱导公式及三角函数的单调性,可判断(3);根据数列前n项和与通项公式的关系,可判断(4);根据已知求出S4,可判断(5).
解答 解:(1)非零常数数列既是等差数列也是等比数列,故错误;
(2)在△ABC中,若sin2A+sin2B=sin2C,则a2+b2=c2,则△ABC为直角三角形,故正确;
(3)若A,B为锐角三角形的两个内角,
锐角三角形,所以A+B>$\frac{π}{2}$即:$\frac{π}{2}$>A>$\frac{π}{2}$-B>0,
所以sinA>cosB,
同理sinB>cosA,所以tanAtanB=$\frac{sinAsinB}{cosAcosB}$>1,正确;
(4)若Sn为数列{an}的前n项和,则此数列的通项an=Sn-Sn-1(n>1),a1=S1,(n=1),故错误.
(5)等比数列{an}的前n项和为Sn,S2=3,S6=63,
则公比q≠1,
即$\left\{\begin{array}{l}\frac{{a}_{1}(1-{q}^{2})}{1-q}=3\\ \frac{{a}_{1}(1-{q}^{6})}{1-q}=63\end{array}\right.$,解得:$\left\{\begin{array}{l}{a}_{1}=1\\ q=2\end{array}\right.$,或$\left\{\begin{array}{l}{a}_{1}=-3\\ q=-2\end{array}\right.$
则S4=15,故正确;
故答案为:(2)(3)(5).
点评 本题以命题的真假判断与应用为载体,考查了等差(比)数列的定义,数列的和及通项公式,正弦定理等知识点,难度中档.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2或0 | B. | 0 | C. | -2或0 | D. | -2或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
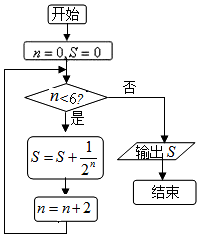
| A. | $\frac{21}{16}$ | B. | $\frac{85}{64}$ | C. | $\frac{63}{32}$ | D. | $\frac{127}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3≤x≤8,且x∈N | B. | 2≤x≤8,且x∈N | C. | 8≤x≤12,且x∈N | D. | 10≤x≤15,且x∈N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≥0}\\{2x-y-2≤0}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≥0}\\{2x-y-2≥0}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≤0}\\{2x-y-2≤0}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x+y-1≥0}\\{x-2y+2≤0}\\{2x-y-2≥0}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com