Question

函数的一段图象如图所示．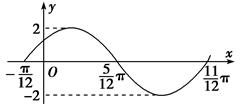

(1)求函数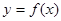的解析式；
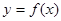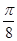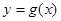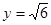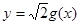(2)将函数的图象向右平移个单位，得到的图象，求直线与函数的图象在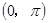内所有交点的坐标．

Answer 1

（1）f(x)＝2sin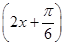（2）交点坐标为.

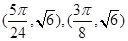解析试题分析：解：(1)由图知A＝2，T＝π，于是ω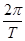＝＝2，      3分
将y＝2sin 2x的图象向左平移，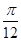
得y＝2sin(2x＋φ)的图象．
于是φ＝2·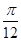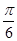＝，                                 4分
∴f(x)＝2sin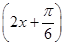.                              5分
(2)依题意得
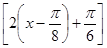g(x)＝2sin=2sin.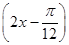
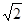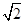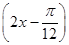故y＝g(x)＝2sin.          7分
由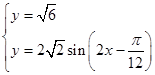
得sin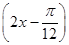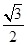＝.                     8分
∴2x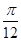－＝＋2kπ或2x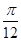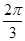－＝＋2kπ(k∈Z)，
∴x＝＋kπ或x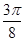＝＋kπ(k∈Z)．      10分
∵x∈(0，π)，
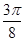∴x＝或x＝.                        11分
∴交点坐标为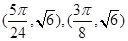.       12分
考点：三角函数图像以及性质
点评：解决的关键是利用整体的思想结合三角函数的性质熟练的求解其解析式以及交点，属于基础题。