
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 甲 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 乙 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
分析 (1)由成绩统计表能求出甲、乙两组研发新产品的成绩的平均数和方差,由$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,得甲的研发水平好.
(2)由已知得甲组研发成功的概率p1=$\frac{10}{15}$=$\frac{2}{3}$,乙组研发成功的概率p2=$\frac{9}{15}$=$\frac{3}{5}$,由此能估算恰有一组研发成功有概率.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{15}(1×10)$=$\frac{2}{3}$,
$\overline{{x}_{乙}}$=$\frac{1}{15}$(9×1)=$\frac{3}{5}$,
${{S}_{甲}}^{2}$=$\frac{1}{15}$[(1-$\frac{2}{3}$)2×10+(0-$\frac{2}{3}$)2×5]=$\frac{2}{9}$,
${{S}_{乙}}^{2}$=$\frac{1}{15}$[(1-$\frac{3}{5}$)2×9+(0-$\frac{3}{5}$)2×6]=$\frac{6}{25}$,
∵$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,
∴甲的研发水平好.
(2)由已知得甲组研发成功的概率p1=$\frac{10}{15}$=$\frac{2}{3}$,乙组研发成功的概率p2=$\frac{9}{15}$=$\frac{3}{5}$,
∴企业安排甲、乙两组各自研发一种新产品,
估算恰有一组研发成功有概率p=$\frac{2}{3}(1-\frac{3}{5})+(1-\frac{2}{3})×\frac{3}{5}$=$\frac{7}{15}$.
点评 本题考查平均数、方差、概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q为假 | B. | (¬p)∧(¬q)为真 | C. | (¬p)∨(¬q)为假 | D. | (¬p)∧q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=-sin2x | C. | $y=-cos\frac{x}{2}$ | D. | $y=-sin\frac{x}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
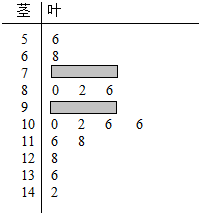 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com