
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上都可能 |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
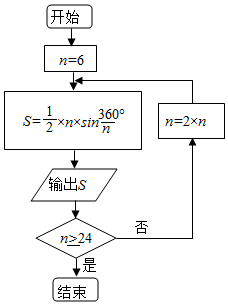 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )| A. | 2.598,3,3.1048 | B. | 2.598,3,3.1056 | C. | 2.578,3,3.1069 | D. | 2.588,3,3.1108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com