
分析 (1)由两点的坐标求得kMN=-1,kPQ,=-1,可得两直线平行;
(2)直接由直线方程的点斜式求得直线PQ的方程.
解答 解:(1)∵M(1,1),N(3,-1),P(4,0),Q(2,2),
∴${k}_{MN}=\frac{-1-1}{3-1}=-1$
,${k}_{PQ}=\frac{2-0}{2-4}=-1$,则kMN=kPQ,
又MNPQ为四边形,
∴直线MN与直线PQ平行;
(2)∵${k}_{PQ}=\frac{2-0}{2-4}=-1$,P(4,0),
由直线方程的点斜式可得PQ:y-0=-1×(x-4),即x+y-4=0.
点评 本题考查由两点坐标求直线的斜率,考查直线方程的点斜式,训练了两直线平行与斜率的关系,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,3} | C. | {1,4} | D. | {1,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
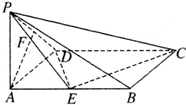 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 算法是某个问题的解决过程 | B. | 算法执行后可以不产生确定的结果 | ||
| C. | 解决某类问题的算法不是唯一的 | D. | 算法可以无限的操作下去不停止 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$]∪[2,+∞) | B. | [$\frac{1}{2}$,1] | C. | (-∞,$\frac{1}{2}$]∪[1,+∞) | D. | (-∞,-1]∪[$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
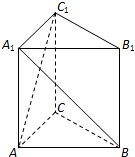 如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com