
分析 设P(x,y),M(x0,y0),根据中点坐标公式,利用代入法进行化简即可.
解答 解:设P(x,y),M(x0,y0),因为M是线段OP的中点,
则有$\left\{\begin{array}{l}{x_0}=\frac{x}{2}\\{y_0}=\frac{y}{2}\end{array}\right.⇒\left\{\begin{array}{l}x=2{x_0}\\ y=2{y_0}\end{array}\right.$,
所以$2×{(2{x_0})^2}-{({y_0})^2}=1$,即$8x_0^2-y_0^2=1$,
故答案为8x2-4y2=1.
点评 本题主要考查点的轨迹方程的求解,设出点的坐标,根据中点坐标关系,利用代入法是解决本题的关键.难度不大.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
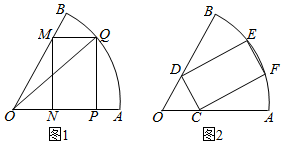 如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.
如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com