
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,连接AB,再作出以AB为直径的圆,在圆上取C点并连接OC,则根据已知条件知道$\overrightarrow{OC}$=$\overrightarrow{c}$,所以$|\overrightarrow c|$最大时,OC为该圆的直径,所以便得到$|\overrightarrow c|$的最大值为$\sqrt{2}$.
解答 解:∵向量$\overrightarrow c$满足$(\overrightarrow c-\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,
∴$(\overrightarrow{c}-\overrightarrow{a})⊥(\overrightarrow{c}-\overrightarrow{b})$;
∴如图设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,连接AB,再作出以AB为直径的圆,在圆上取C点并连接OC,
则根据已知条件知道$\overrightarrow{OC}$=$\overrightarrow{c}$,
所以$|\overrightarrow c|$最大时,OC为该圆的直径,
根据图形及已知条件,此时|$\overrightarrow{OC}$|=$\sqrt{2}$,则$|\overrightarrow c|$的最大值为$\sqrt{2}$.
故选B
点评 本题考查两非零向量垂直的充要条件,圆上的点和直径两端点的连线互相垂直,以及向量的减法运算.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
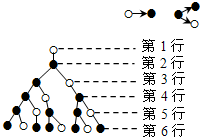 分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照
分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com