
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 若an<an+1,则第n+1题一定答对,当n=1时,还可得到第一题一定答错,若an>an+1,则第n+1题一定答错,当n=1时,还可得到第一题一定答对,进而可判断四个结论的正误,得到答案.
解答 解:若a1<a2,则第一题一定答错,第二题一定答对,
若a2<a3,则第三题一定答对,
…
故若a1<a2<…<a10,则必是第一题答错,其余题均答对,即①正确;
a9>a10,则第十题一定答错,
…
a1>a2,则第二题一定答错,第一题一定答对,
故若a1>a2>…>a10,则必是第一题均答对,其余题均答错,即②正确;
a5=a10=1,故④正确;
故选:D.
点评 本题以命题的真假判断为载体,考查了归纳推理,其中根据题意分析出若an<an+1,则第n+1题一定答对,当n=1时,还可得到第一题一定答错,若an>an+1,则第n+1题一定答错,当n=1时,还可得到第一题一定答对,是解答的关键.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
 将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$
将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
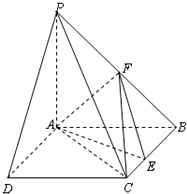 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC.
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com