
| ������λ��ǧ��Ԫ�� | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| Ƶ�� | 2 | 1 | 2 | 4 | 1 |
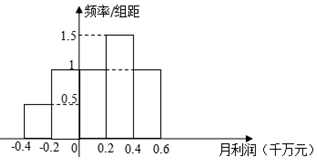
���� ������Ƶ�ʷֲ�ֱ��ͼ�������10�������㳡����ƽ������ͽ�10����Զ���̶ӵ���ƽ������
�������������x��y�������������������Ŀ������֮��Ϊz����z=0.02x+0.16y���ɴ��������Թ滮�������˾Ͷ�����㳡4ǧ��Ԫ��Զ���̶�2ǧ��Ԫʱ��������Ŀ����ƽ������֮�����
��� �⣺����10�������㳡����ƽ������Ϊ��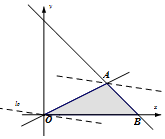
$\frac{-0.2��2-0.1��1+0��2+0.1��4+0.3��1}{10}=0.02$��ǧ��Ԫ������..��3�֣�
��10����Զ���̶ӵ���ƽ������Ϊ��
-0.3��0.2��0.5-0.2��0.1��1+0.1��0.2��1+0.3��0.2��1.5+0.5��0.2��1=0.16��ǧ��Ԫ������6�֣�
�����������x��y���������Ϊ$\left\{\begin{array}{l}x��0\\ y��0\\ x+y��6\\ x��2y\end{array}\right.$����..��8�֣�
��������Ŀ������֮��Ϊz����z=0.02x+0.16y������������9�֣�
��ͼ��ʾ����ֱ��l0��0.02x+0.16y=0��ƽ��ֱ��l0֪�����Aʱ��zȡ���ֵ����10�֣�
��$\left\{\begin{array}{l}x+y=6\\ x=2y\end{array}\right.$����$\left\{\begin{array}{l}x=4\\ y=2\end{array}\right.$������A������Ϊ��4��2������..��11�֣�
��ʱz�����ֵΪz=0.08+0.32=0.4��ǧ��Ԫ����
���Թ�˾Ͷ�����㳡4ǧ��Ԫ��Զ���̶�2ǧ��Ԫʱ��������Ŀ����ƽ������֮�����..��12�֣�
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã��������Թ滮��Ӧ�ã����е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 24 | C�� | 30 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{\sqrt{6}��\sqrt{7}}]$ | B�� | $��{0��\sqrt{7}}]$ | C�� | $��{\frac{{2\sqrt{42}}}{5}��\sqrt{7}}]$ | D�� | ��6��7] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{12}$ | C�� | $\frac{1}{9}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
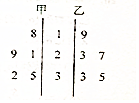 �ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ���
�ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com