
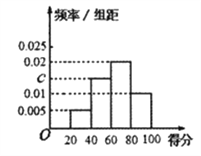
����Ŀ��ijУΪ�˽�У��ȫ����ϵ�л�ij�Ч����ȫУѧ��������һ�ΰ�ȫ��ʶ���ԣ����ݲ��Գɼ��������ϸ������ϸ������ȼ���ͬʱ����Ӧ�ȼ��������������ϸ�5�֣������ϸ�0��.�������ȡ����ѧ���Ĵ����ͳ�ƽ������Ӧ��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
�ȼ� | ���ϸ� | �ϸ� | ||
�÷� |
|
|
|
|
Ƶ�� | 6 |
| 24 |
|
������![]() ��
�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
�����÷ֲ�����ķ������������ȼ�Ϊ���ϸ͡����ϸ�ѧ���������ȡ10�˽�����̸.���ٴ���10������ѡ4�ˣ�����ѡ4�˵������ܷ�Ϊ![]() ����
����![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
����ij����������ָ��![]() ��
��![]() ������
������![]() ��ʾ
��ʾ![]() �ķ����������У��ȫ������ij�Ч.��
�ķ����������У��ȫ������ij�Ч.��![]() �����϶����������Ч�ģ������϶��������Ч��Ӧ������ȫ��������.�ڣ��������£��жϸ�У�Ƿ�Ӧ������ȫ����������
�����϶����������Ч�ģ������϶��������Ч��Ӧ������ȫ��������.�ڣ��������£��жϸ�У�Ƿ�Ӧ������ȫ����������
���𰸡���1��![]() ��
�� ![]() ����2����3��������.
����2����3��������.
�������������������1������Ƶ�ʷֲ�ֱ��ͼ�����ʼ��ɵó�����2���������ȼ�Ϊ���ϸ͡����ϸ�ѧ���������ȡ10�˽�����̸�����С����ϸ�ѧ��![]() ���ϸ�ѧ����=6��������ɵæ�=0��5��10��15��20�����á������ηֲ��С��ļ��㹫ʽ���ɵó����ʣ������ó��ֲ�������ѧ��������3������D�����㹫ʽ���ɵó����ɵ�
���ϸ�ѧ����=6��������ɵæ�=0��5��10��15��20�����á������ηֲ��С��ļ��㹫ʽ���ɵó����ʣ������ó��ֲ�������ѧ��������3������D�����㹫ʽ���ɵó����ɵ�![]() ,���ɵó����ۣ�
,���ɵó����ۣ�
�����������1����Ƶ�ʷֲ�ֱ��ͼ��֪���÷���![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��
��
�ʳ�ȡ��ѧ�������Ϊ�� ![]() ��
��
����Ƶ�ʷֲ�ֱ��ͼ��֪���÷���![]() ��Ƶ��Ϊ0.2��
��Ƶ��Ϊ0.2��
����![]() ��
��
��![]() ����
����![]() ��
��
����![]() .
.
![]() .
.
��2�������ϸ��롰�ϸ���������Ϊ24��36=2��3��
��˳�ȡ��10���С����ϸ���4�ˣ����ϸ���6��.
����![]() ��20��15��10��5��0��5�ֿ��ܵ�ȡֵ.
��20��15��10��5��0��5�ֿ��ܵ�ȡֵ.
![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
![]() ��
�� ![]() .
.
![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 20 | 15 | 10 | 5 | 0 |
|
|
|
|
|
|
����![]() .
.
��3���ɣ�2���ɵ�
![]() ��
��
����![]() ��
��
��������Ϊ��У�İ�ȫ���������Ч�ģ�����Ҫ������ȫ��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
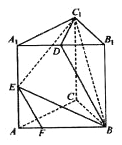
����Ŀ����������ABC-A1B1C1�У�AB=BC=CA=AA1=2������AA1��ƽ��ABC����D��E�ֱ�����A1B1��AA1���е㣬��F����AB�ϣ���AF=![]() AB��
AB��
��1����֤��EF��ƽ��BDC1��
��2��������D-BEC1�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��4cos��x��sin(��x��![]() )(��>0)����С������Ϊ����
)(��>0)����С������Ϊ����
(1)������ֵ��
(2)����f(x)������[0��![]() ]�ϵĵ����ԣ�
]�ϵĵ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���y=f��x���ĵ�����Ϊf�䣨x��������f�䣨x����f��x������f��0��=1����ʽf��x����ex�Ľ⼯Ϊ�� ��
A.�����ޣ�e4��
B.��e4 �� +�ޣ�
C.�����ޣ�0��
D.��0��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��2lnx��
��1����֤��f��x���ڣ�1��+�ޣ��ϵ���������
��2����f��x����2tx�� ![]() ��x�ʣ�0��1]�ں��������ʵ��t��ȡֵ��Χ��
��x�ʣ�0��1]�ں��������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ200��ְ��������ֲ������ͼ����Ҫ���г�ȡ40��ְ������������ϵͳ����������ȫ��ְ�������1��200��ţ��������˳��ƽ����Ϊ40�����ĺ���Ϊ28�����8�����ĺ���Ӧ��a�����÷ֲ������������50�����������Ӧ��ȡb�ˣ���ôa+b���ڣ� �� 
A.46
B.45
C.70
D.69
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x��=  ��������5�����ۣ� ����ȡx1 �� x2��[0��+�ޣ�������|f��x1����f��x2��|��2��
��������5�����ۣ� ����ȡx1 �� x2��[0��+�ޣ�������|f��x1����f��x2��|��2��
�ں���y=f��x��������[4��5]�ϵ���������
��f��x��=2kf��x+2k����k��N+������һ��x��[0��+�ޣ��������
�ܺ���y=f��x����ln��x��1����3����㣻
��������x�ķ���f��x��=m��m��0������ֻ��������ͬʵ��x1 �� x2 �� ��x1+x2=3��
������������ȷ���۵������ �� ����д��ȫ����ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x���ĵ�����Ϊf�䣨x�����������x��R����3f�䣨x����f��x���������� ��
A.3f��3ln2����2f��3ln3��
B.3f��3ln2����2f��3ln3���Ĵ�С��ȷ��
C.3f��3ln2��=2f��3ln3��
D.3f��3ln2����2f��3ln3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У��ڽ�A��B��C�ĶԱ߷ֱ���a��b��c����a2��b2��
�У��ڽ�A��B��C�ĶԱ߷ֱ���a��b��c����a2��b2��![]() ab=c2.
ab=c2.
��1����C��
��2����cos Acos B��![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com