
| A. | (-∞,0] | B. | (-∞,1] | C. | (-∞,2] | D. | (-∞,3] |
分析 求出函数的导数,通过a的符号,求解函数的极值,判断函数的零点个数.
解答 解:f′(x)=3x2-2ax=3x(x-$\frac{2a}{3}$),
当a<0时,f(x)在x=$\frac{2a}{3}$处取得极大值f($\frac{2a}{3}$)=4-$\frac{4}{27}$a3>0,
在x=0处取得极小值f(0)=4>0,此时有一个零点,满足条件;
当a=0时显然满足条件,
当a>0时,在x=0处取得极大值4,在x=$\frac{2a}{3}$处取得极小值4-$\frac{4}{27}$a3≥0,
解得a≤3,
故选:D.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的零点个数的关系,考查分类讨论思想以及转化思想的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
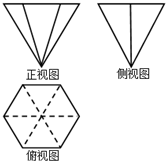 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,1)上是增函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 偶函数,且在(0,1)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标伸长到原来的2倍,再向左平行移动$\frac{π}{3}$个单位长度 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍,再向左平行移动$\frac{π}{3}$个单位长度 | |
| C. | 横坐标缩短到原来的$\frac{1}{2}$倍,再向左平行移动$\frac{π}{6}$个单位长度 | |
| D. | 横坐标缩短到原来的$\frac{1}{2}$倍,再向右平行移动$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com