
| A. | 2007 | B. | $\frac{1}{1009}$ | C. | 1 | D. | $\frac{2017}{2}$ |
分析 根据等比数列的性质得和f(x)+f(-x)=1,即可求出答案.
解答 解∵$f(x)=\frac{e^x}{{{e^x}+1}}$,
∴$f(-x)+f(x)=\frac{e^x}{{{e^x}+1}}+\frac{{{e^{-x}}}}{{{e^{-x}}+1}}=1$,
∵数列{an}是等比数列,
∴${a_1}{a_{2017}}={a_2}{a_{2016}}=…={a_{1008}}{a_{1010}}=a_{1009}^2=1$,
∴设S2017=f(lna1)+f(lna2)+…+f(lna2017)①,
∵S2017=f(lna2017)+f(lna2016)+…+f(lna1)②,
①+②得2S2017=2017,
∴${S_{2017}}=\frac{2017}{2}$,
故选:D.
点评 考查学生利用等比数列性质的能力,以及指数对数函数的综合运用能力.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 92 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
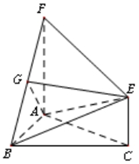 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com