
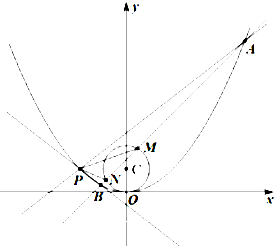
 设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.
设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.
|
| (-2-0)2+(1+b)2 |
|
| (2k+1)2-(-2k+1)2 |
| 4k+2-(-4k+2) |
| |t-3| | ||
|
|
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| -t2+2t+1 |
| 1 |
| 2 |
| |t-3| | ||
|
| 2 |
| -t2+2t+1 |
| 1 |
| 2 |
| (t-3)2•(-t2+2t+1 |
| 2 |
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
3+
| ||
| 4 |
|
3-
| ||
| 2 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
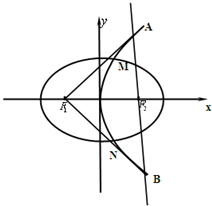 已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
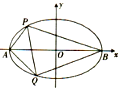 如图,以
如图,以
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AM |
| AN |
| PQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
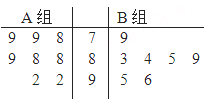 天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com