
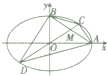
 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| S1 |
| S2 |
| S1 |
| S2 |
| |CM| |
| |DM| |
| ||||||||
|
| 1-e2 |
| 1-e2 |
| 1-e2 |
| 1-e2 |
| a2 |
| 2 |
| 2 |
| 2 |
| 2(1-e2) |
| 2 |
| 2(1-e2) |
| S1 |
| S2 |
| |CM| |
| |DM| |
| ||||||||
|
| ||
|
| 2 |


科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| X | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P1 | P2 | P3 | P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 3 |
| 2 |
| 1 |
| lnx |
| 1 |
| x-1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示的茎叶图记录了甲、乙两组各四名同学的植树的棵数;乙组有一个数据模糊,用X表示.
如图所示的茎叶图记录了甲、乙两组各四名同学的植树的棵数;乙组有一个数据模糊,用X表示.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<
如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)
将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)| 5 |
| 4 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
| 7 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com