考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由已知得
f′(x)=,由此利用分类讨论思想和导数性质能求出实数a的值.
(Ⅱ)由已知得
-<?(x+1)lnx-2(x-1)>0.令F(x)=(x+1)lnx-2(x-1),由此利用导数性质能证明当1<x<2时,不等式
-
<
恒成立.
解答:
(1)解:∵f(x)=lnx-
,∴
f′(x)=,
①若a≥-1,则x+a≥0,即f'(x)≥0在[1,e]上恒成立,
f(x)在[1,e]上为增函数,
∴
[f(x)]min=f(1)=-a=,∴
a=-(舍去). …(2分)
②若a≤-e,则x+a≤0,即f'(x)≤0在[1,e]上恒成立,
f(x)在[1,e]上为减函数,
∴
[f(x)]min=f(e)=1-=,∴
a=-(舍去). …(4分)
③若-e<a<-1,当1<x<-a时,f'(x)<0,
∴f(x)在(1,-a)上为减函数,
,
∴
f(x)在(-a,e)上为增函数,∴
a=-,
综上所述,
a=-…(6分)
(Ⅱ)证明:∵1<x<2,∴
-<?(x+1)lnx-2(x-1)>0.
令F(x)=(x+1)lnx-2(x-1),(8分)
∴F′(x)=lnx+
-2=
lnx+-1…(9分).
∴当x∈[1,2]时,F′(x)≥0,
∴F(x)在(1,2)上单调递增,
∴F(x)>F(1)=0,
∴(x+1)lnx-2(x-1)>0.
∴
-<(1<x<2)恒成立. …(12分)
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 如图,三棱柱ABC-A1B1C1为直三棱柱,D是AB中点,AA1=AC=BC=
如图,三棱柱ABC-A1B1C1为直三棱柱,D是AB中点,AA1=AC=BC=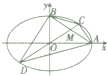 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E: 如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,
如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,