Question

如图，三棱柱ABC-A₁B₁C₁为直三棱柱，D是AB中点，AA₁=AC=BC=

5

6

AB=5．
（1）证明：BC₁∥平面A₁CD；
（2）在线段BC₁上是否存在一点M，使得二面角M-A₁D-C的余弦值为

38

19

，若存在，求出BM的长，若不存在，请说明理由．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）连接AC₁交A₁C于点E，则点E是AC₁的中点，连接DE，又D是AB中点，利用三角形的中位线定理可得：DE∥BC₁．再利用线面平行的判定定理即可得出．
（2）取A₁B₁的中点F，可得DF⊥平面ABC，由于AA₁=AC=BC=

5

6

AB=5，可得CD⊥AB，AB=6．建立如图所示的空间直角坐标系．假设在线段BC₁上存在一点M，使得二面角M-A₁D-C的余弦值为

38

19

．设

BM

=λ

BC1

，（0≤λ≤1）．可得

DM

=

DB

+λ

BC1

=（3-3λ，4λ，5λ）．利用平面的法向量的夹角即可得出．

解答： （1）证明：连接AC₁交A₁C于点E，
则点E是AC₁的中点，连接DE，
∵D是AB中点，∴DE∥BC₁．
∵DE?平面A₁CD，BC₁?平面A₁CD，
∴BC₁∥平面A₁CD；
（2）解：取A₁B₁的中点F，
则DF⊥平面ABC，
∴DF⊥AB，DF⊥DC．
∵AA₁=AC=BC=

5

6

AB=5，
∴CD⊥AB，AB=6．
∴B（3，0，0），C（0，4，0），A₁（-3，0，5），C₁（0，4，5）．
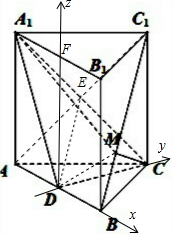
建立如图所示的空间直角坐标系．
假设在线段BC₁上存在一点M，使得二面角M-A₁D-C的余弦值为

38

19

．
设

BM

=λ

BC1

，（0≤λ≤1）．
∴

DM

=

DB

+λ

BC1

=（3，0，0）+λ（-3，4，5）=（3-3λ，4λ，5λ）．
设平面DMA₁的法向量

m

=（x₁，y₁，z₁）．
则

m • DA1 =-3x1+5z1=0 m • DM =(3-3λ)x1+4λy1+5λz1=0

，
令x₁=5，则z₁=3，y₁=-

15

4λ

．
∴

m

=(5，-

15

4λ

，3)．
设平面CDA₁的法向量

n

=（x₂，y₂，z₂）．
则

n • DC =4y2=0 n • DA1 =-3x2+5z2=0

，令x₂=5，解得y₂=0，z₂=3．
∴

n

=（5，0，3）．
∴cos＜

m

，

n

＞=

m • n

| m || n |

=

34

34 • 34+(- 15 4λ )2

=

38

19

．
解得λ=

15

68

．
因此在线段BC₁上存在一点M(

159

68

，

30

34

，

75

68

)，使得二面角M-A₁D-C的余弦值为

38

19

，
|

BM

|=

15

68

×|

BC1

|=

15

68

×

(-3)2+42+52

=

75 2

68

．

点评：本题考查了直三棱柱的性质、三角形的中位线定理、线面平行的判定定理，考查了通过建立空间直角坐标系利用平面的法向量的夹角求二面角的方法，考查了空间想象能力，考查了推理能力和计算能力，属于难题．