Question

15．设函数f（x）=$\left\{\begin{array}{l}{x（x-1）．（x≥0）}\\{-\frac{9}{40}x（x-1）．（x＜0）}\end{array}\right.$
（1）若方程f（x）=m有两个不同的解，求实数m的值，并解此方程；
（2）当x∈（-b，b）（b＞0）时，求函数f（x）的值域．

Answer 1

分析 （1）可求得f（0）=0，f（1）=0，f（$\frac{1}{2}$）=-$\frac{1}{4}$，f（-$\frac{2}{3}$）=-$\frac{1}{4}$；且f（x）在（-∞，0）上递增，在（0，$\frac{1}{2}$）上递减，在（$\frac{1}{2}$，+∞）上递增；从而可得当m=0或m=-$\frac{1}{4}$时，方程f（x）=m有两个不同的解．再代入求解即可．
（2）由（1）可知，作出函数f（x）的图象，从而以0＜b≤$\frac{1}{2}$，$\frac{1}{2}$＜b≤$\frac{2}{3}$，$\frac{2}{3}$＜b≤1，b＞1讨论函数的值域即可．

解答 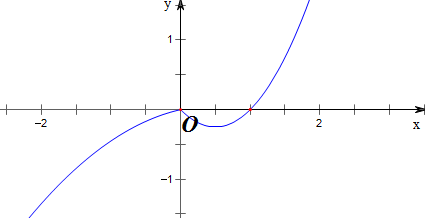解：（1）∵f（0）=0，f（1）=0，f（$\frac{1}{2}$）=-$\frac{1}{4}$，
当x＜0时，f（-$\frac{2}{3}$）=-$\frac{1}{4}$；
又∵f（x）在（-∞，0）上递增，在（0，$\frac{1}{2}$）上递减，在（$\frac{1}{2}$，+∞）上递增；
∴当m=0或m=-$\frac{1}{4}$时，方程f（x）=m有两个不同的解．
当m=0时，方程的解为0，1；
当m=-$\frac{1}{4}$时，方程的解为$\frac{1}{2}$，-$\frac{2}{3}$；
（2）由（1）可知，函数f（x）的图象如图所示，
①当0＜b≤$\frac{1}{2}$时，
∵f（-b）-f（b）=-$\frac{9}{40}$b（b+1）-b（b-1）
=-$\frac{1}{40}$b（49b-31）＞0，
此时函数f（x）的值域为（b（b-1），0]；
②当$\frac{1}{2}$＜b≤$\frac{2}{3}$时，
∵f（-b）≥f（$\frac{1}{2}$），
∴函数f（x）的值域为[-$\frac{1}{4}$，0]；
③当$\frac{2}{3}$＜b≤1时，
∵f（-b）＜f（$\frac{1}{2}$），且f（b）≤0；
∴函数f（x）的值域为（-$\frac{9}{40}$b（b+1），0]；
④当b＞1时，
∵f（-b）＜f（$\frac{1}{2}$），且f（b）＞0；
∴函数f（x）的值域为（-$\frac{9}{40}$b（b+1），b（b-1））．

点评 本题考查了函数的图象的应用及方程的根与函数的图象的关系应用，同时考查了分类讨论的思想应用，属于基础题．