
【题目】已知函数![]() 是定义域为
是定义域为![]() 的偶函数,且满足
的偶函数,且满足![]() ,当
,当![]() 时,
时,![]() ,则函数
,则函数![]() 在区间
在区间![]() 上零点的个数为( )
上零点的个数为( )
A.9B.10C.18D.20
【答案】B
【解析】
由已知可得函数f(x)的周期与对称轴,函数F(x)=f(x)![]() 在区间
在区间![]() 上零点的个数等价于函数f(x)与g(x)
上零点的个数等价于函数f(x)与g(x)![]() 图象在
图象在![]() 上交点的个数,作出函数f(x)与g(x)的图象如图,数形结合即可得到答案.
上交点的个数,作出函数f(x)与g(x)的图象如图,数形结合即可得到答案.
函数F(x)=f(x)![]() 在区间
在区间![]() 上零点的个数等价于函数f(x)与g(x)
上零点的个数等价于函数f(x)与g(x)![]() 图象在
图象在![]() 上交点的个数,
上交点的个数,
由f(x)=f (2﹣x),得函数f(x)图象关于x=1对称,
∵f(x)为偶函数,取x=x+2,可得f(x+2)=f(﹣x)=f(x),得函数周期为2.
又∵当x∈[0,1]时,f(x)=x,且f(x)为偶函数,∴当x∈[﹣1,0]时,f(x)=﹣x,
g(x)![]() ,
,
作出函数f(x)与g(x)的图象如图:
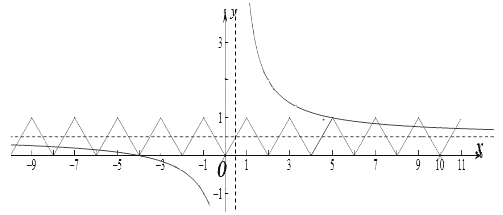
由图可知,两函数图象共10个交点,
即函数F(x)=f(x)![]() 在区间
在区间![]() 上零点的个数为10.
上零点的个数为10.
故选:B.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加某项服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为多面体,平面
为多面体,平面![]() 与平面
与平面![]() 垂直,点
垂直,点![]() 在线段
在线段![]() 上,
上,![]()
![]() 都是正三角形.
都是正三角形.

(1)证明:直线![]() ∥面
∥面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() ,若不存在请说明理由,若存在请求出
,若不存在请说明理由,若存在请求出![]() 点所在的位置。
点所在的位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校一位教师要去某地参加全国数学优质课比赛,已知他乘火车、轮船、汽车、飞机直接去的概率分别为0.3、0.1、0.2、0.4.
(1)求他乘火车或乘飞机去的概率;
(2)他不乘轮船去的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系O﹣xyz中,已知正四棱锥P﹣ABCD的所有棱长均为6,底面正方形ABCD的中心在坐标原点,棱AD,BC平行于x轴,AB,CD平行于y轴,顶点P在z轴的正半轴上,点M,N分别在线段PA,BD上,且![]() .
.

(1)求直线MN与PC所成角的大小;
(2)求锐二面角A﹣PN﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com